Misure di Tendenza Non Centrale, Forma della Distribuzione e Outlier

Misure di Tendenza Non Centrale

Consideriamo, per il momento, solo variabili quantitative. L'idea di mediana può essere estesa e portare a considerare indicatori di tendenza non centrale, ovvero valori che dividono la distribuzione in due parti non uguali e che, quindi, non giacciono al centro di essa.

Quartili

• Si definisce primo quartile Q1 di una distribuzione (o di una variabile) un valore che divide in due parti la distribuzione, lasciando alla sua sinistra il 25% dei dati (ovvero, una frequenza relativa pari a 0.25) e, quindi, il 75% (cioè una frequenza relativa pari a 0.75) alla sua destra.
• Si definisce terzo quartile Q3 di una distribuzione (o di una variabile) un valore che divide in due parti la distribuzione, lasciando alla sua sinistra il 75% dei dati (ovvero, una frequenza relativa pari a 0.75) e, quindi, il 25% (cioè una frequenza relativa pari a 0.25) alla sua destra.

I due quartili, insieme alla mediana (che assume quindi il ruolo di secondo quartile), dividono la distribuzione in quattro parti uguali, a ciascuna delle quali compete una frequenza relativa pari a 0.25. Dal punto di vista operativo, per i quartili valgono le stesse considerazione fatte con riferimento alla mediana, con le ovvie modifiche (ovvero, la frequenza cumulata di riferimento, che per la mediana era 0.5, ora è 0.25 o 0.75).

Esempio 1: Campione di 200 Studenti Universitari

ESEMPIO 1 (già visto): campione di 200 studenti universitari, Z=numero di componenti della famiglia dello studente, con la seguente distribuzione:

modalità freq.assol. freq. relat. freq. cumul. 1 20 0.100 0.100 2 55 0.275 0.375 3 70 0.350 0.725 4 50 0.250 0.975 6 5 0.025 1

Per la ricerca del primo quartile la frequenza cumulata di riferimento è, per quanto detto, 0.25; poiché questo valore non è presente, il primo quartile è 2 (primo valore in cui la frequenza cumulata è maggiore di 0.25). Analogamente, il terzo quartile è 4 (primo valore in cui la frequenza cumulata è maggiore di 0.75).

Esempio 2: Numero di Esami Superati

ESEMPIO 2: campione di 200 studenti universitari, S=numero di esami superati, la cui distribuzione è data dalla tabella che segue:

modalità freq.assol. freq. relat. freq. cumul. 1 2 0.010 0.010 4 54 0.270 0.280 5 94 0.470 0.750 6 30 0.150 0.900 7 20 0.100 1

Anche in questo caso, tra le frequenze cumulate non compare il valore 0.25, per cui il primo quartile è 4. Al contrario, poiché è presente la frequenza cumulata 0.75, il terzo quartile è un qualunque valore compresotra 5 e 6 (estremi inclusi), in maniera del tutto analoga a quanto avviene per la mediana Convenzionalmente, sceglieremo come valore unico del terzo quartile il punto medio 5.5.

Esempio 3: Tempo di Raggiungimento dell'Università

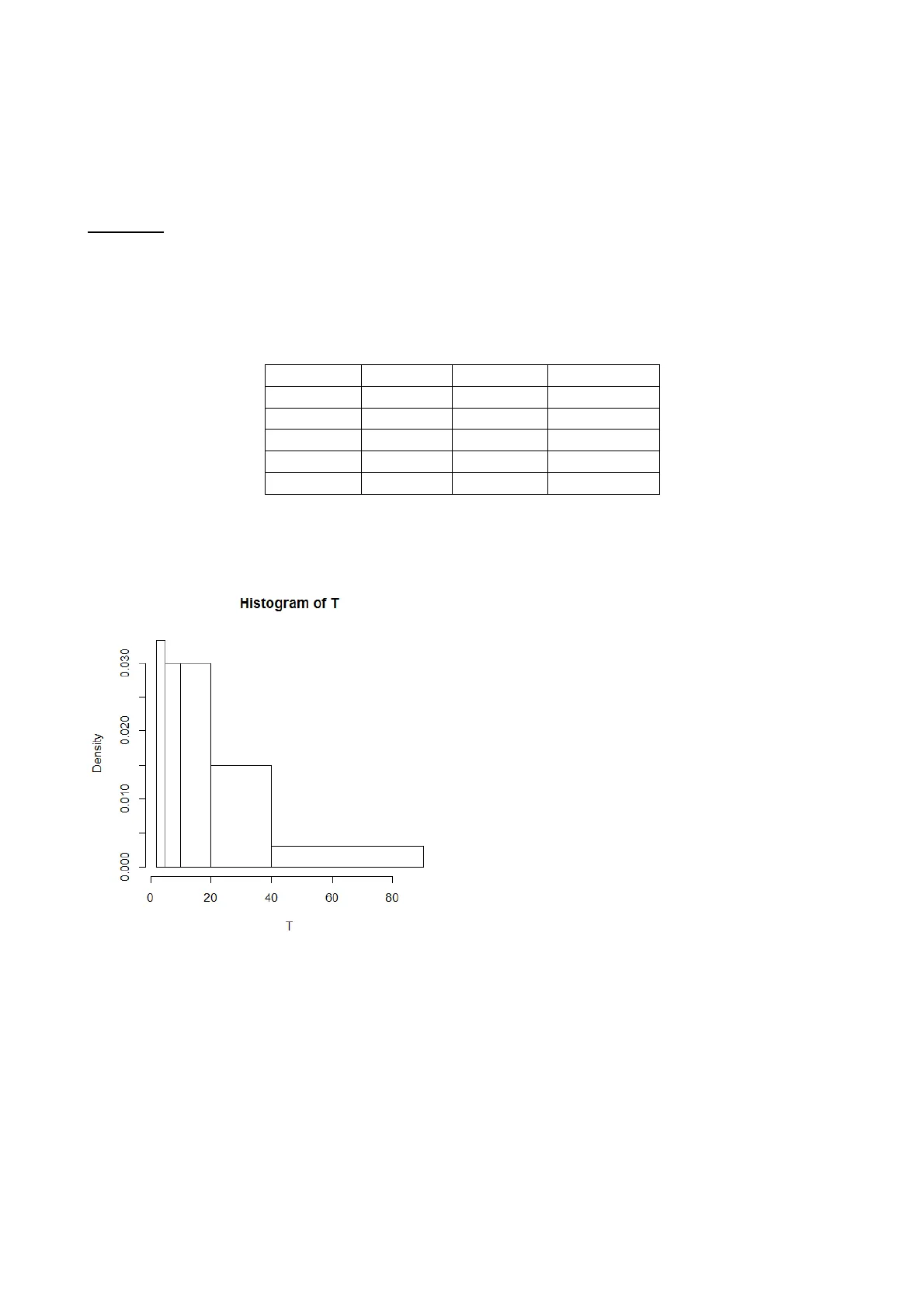
ESEMPIO 3: sempre con riferimento al campione di 200 studenti, consideriamo la variabile (quantitativa continua) T che rappresenta il tempo (in minuti) impiegato dallo studente per raggiungere, dall'abitazione, l'università. La distribuzione di T è riportata di seguito (per ciascun intervallo, è indicata anche la frequenza cumulata fino a quell'intervallo incluso):

intervallo freq.assol. freq. relat. freq. cumul. [2,5] 20 0.10 0.10 (5,10] 30 0.15 0.25 (10,20] 60 0.30 0.55 (20,40] 60 0.30 0.85 (40,90] 30 0.15 1

Riportiamo anche, per comodità di visualizzazione, il corrispondente istogramma:

Histogram of T 0.030 0.020 Density 0.010 0.000 0 20 40 60 80 T

Il primo quartile è immediato da individuare; infatti, i primi due intervalli hanno complessivamente una frequenza pari a 0.25 (ovvero, i primi due rettangoli dell'istogramma hanno un'area pari a 0.25). Quindi, il punto che divide in due parti la distribuzione, lasciando frequenza 0.25 a sinistra e 0.75 a destra, è il punto 10, che risulta dunque il primo quartile. Il terzo quartile invece cade nell'intervallo (20,40], in quanto la frequenza cumulata fino a 20 è 0.55, la frequenza cumulata fino a 40 è 0.85, per cui il valore 0.75 si raggiunge all'interno di questo intervallo.

Percentili e Quantili

Il concetto di quartile può ulteriormente essere esteso, definendo punti che effettuano divisioni della distribuzione in parti arbitrarie.

• Si definisce quantile di ordine p € (0,1) un punto che divide in due parti la distribuzione, lasciando alla propria sinistra una frequenza relativa pari a p (e quindi a destra una frequenza pari a 1-p).
• Si definiscono i percentili di una distribuzione come quei 99 punti che dividono la distribuzione in 100 parti con la medesima frequenza (pari ovviamente a 0.01).

Chiaramente, il 25-esimo percentile coincide con il primo quartile, ovvero con il quantile di ordine 0.25, così come la mediana è il 50-esimo percentile, ovvero il quantile di ordine 0.5 e così via. Il primo ed il terzo quartile, insieme alla mediana, al massimo (valore più elevato rilevato per la variabile nel campione) ed al minimo (valore più piccolo rilevato), costituiscono i cosiddetti cinque numeri di sintesi della distribuzione e forniscono informazioni rilevanti su di essa, in particolare con riferimento alla sua forma (simmetria o asimmetria).

OSSERVAZIONE: gli indicatori di tendenza non centrale introdotti (in particolare i quartili) possono, come la mediana, essere calcolati anche per variabili qualitative ordinali, dal momento che richiedono esclusivamente un ordinamento tra le modalità. Ovviamente, come per la mediana, nel caso di non unicità, non ha alcun senso per dati qualitativi ordinali considerare il punto medio.

Forma della Distribuzione

Ci riferiamo qui a dati quantitativi.

• La distribuzione di una variabile è SIMMETRICA se le modalità e le corrispondenti frequenze sono simmetriche rispetto ad un punto (centro di simmetria). Ovviamente, se questo accade, tale punto è tanto la mediana (per simmetria, il 50% dei dati deve giacere alla sinistra di tale punto) quanto la media (tale punto è necessariamente il baricentro della distribuzione).

Con riferimento a dati reali, non si ha praticamente mai a che fare con distribuzioni esattamente simmetriche, ma eventualmente con distribuzione approssimativamente simmetriche, per le quali quindi i comportamenti della distribuzione a destra ed a sinistra di un punto sono solo approssimativamente uguali. E' facile rilevare la simmetria (approssimata) di una distribuzione a partire dal suo grafico (grafico a barre per una variabile discreta o istogramma per una variabile continua); infatti, in caso di (approssimata) simmetria, il grafico appare appunto (approssimativamente) simmetrico, come accade nei due esempi riportati (il primo è un istogramma, il secondo un grafico a barre per una variabile discreta con modalità 0,1,2,3,4,5,6):

Histogram of X 1500 0.3 Density 0.2 0.1 0.0 T 0 2 4 6 0 1 2 3 4 5 6 X

• Una distribuzione è obliqua a destra se la "concentrazione" di unità si riduce procedendo verso valori più elevati; in sostanza, una distribuzione è obliqua a destra se l'istogramma (o il grafico a barre) presenta una più o meno evidente coda verso destra.
• Una distribuzione è obliqua a sinistra se la "concentrazione" di unità si riduce procedendo verso valori più bassi; in sostanza, una distribuzione è obliqua a sinistra se l'istogramma (o il grafico a barre) presenta una più o meno evidente coda verso sinistra.

Il grafico sotto riportato (istogramma) è relativo ad una distribuzione obliqua a destra:

Histogram of X 2.0 1.5 Density 1.0 0.5 0.0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 X

A partire dai 5 numeri di sintesi, possiamo facilmente verificare la simmetria o obliquità della distribuzione. Se una distribuzione è (perfettamente) simmetrica, si ha:

massimo - Q3 = Q1 - minimo Q3 - mediana = mediana - Q1

Inoltre, come detto, media e mediana sono uguali. Se una distribuzione è obliqua a destra, si ha:

massimo - Q3 > Q1 - minimo Q3 - mediana > mediana - Q1 1000 500 O -Inoltre, la media è maggiore della mediana, in quanto risente dei (pochi) valori elevati, a differenza della mediana. A Le disuguaglianze precedenti si invertono per distribuzioni oblique a sinistra.

Outlier

In statistica, vengono chiamati outlier osservazioni nel campione che differiscono in maniera consistente dalla maggior parte dei valori rilevati. Nell'analisi univariata (di cui stiamo trattando adesso), un outlier è quindi un'osservazione con valore della variabile "molto elevato" o "molto basso" (dove i termini elevato e basso sono ovviamente da mettere in relazione ai restanti valori osservati). In certi casi, gli outlier possono essere legati a errori nella rilevazione o nella trasmissione dei dati e quindi, se individuati, andrebbero rimossi. In altri casi sono valori realmente presenti nel campione e quindi devono essere presi in considerazione, anche se talvolta la loro presenza "distorce" alcuni indicatori. Si pensi ad esempio alla media aritmetica che, come visto in precedenza, essendo un indicatore di tendenza centrale non robusto, risente in maniera rilevante della presenza di eventuali outlier; non così, come sappiamo, la mediana. Esistono criteri differenti per stabilire se una certa osservazione è da considerare o meno un outlier. Uno dei più frequentemente adottati, che qui riportiamo, stabilisce che è un outlier un qualunque (eventuale) valore xout rilevato nel campione che soddisfa una delle due disuguaglianze seguenti:

Xout > Q3 + 5 (03 - Q1) Xout < Q1 -5 2 (Q3 - Q1) 3

In sostanza, un'osservazione è un outlier se dista dal terzo quartile (verso l'alto) o dal primo quartile (verso il basso) per più di 1.5 volte la differenza interquartile. In pratica, un'osservazione è un outlier se è posto a distanza "rilevante" dal 50% centrale della distribuzione.

Boxplot

Il boxplot è un grafico che riporta, visivamente, i cinque numeri di sintesi e gli eventuali outlier di una distribuzione. Esso è utile, in particolare, per analizzare la forma della distribuzione, mettendone in evidenza la simmetria o asimmetria. Esistono differenti modi per costruire il boxplot; riportiamo di seguito uno dei più usati, adottato in particolare come scelta di "default" dal software R. Si riportano su un asse verticale il primo quartile, la mediana ed il terzo quartile; si costruisce una "scatola" che ha i lati in corrispondenza ai due quartili, divisa in due da un segmento che corrisponde alla mediana. Si tracciano quindi due "baffi"; il primo al di sopra della scatola, posizionato in corrispondenza al valore più estremo rilevato nel campione che non supera il limite che individua gli outlier, il secondo posto al di sotto della scatola e posizionato in accordo al medesimo criterio. Eventuali outlier vengono poi esplicitamente riportati ed indicati con un piccolo cerchio. Procedendo con due esempi, per comodità distinguiamo il caso in cui non vi sono outlier nella distribuzione da quello in cui essi sono presenti.