Unità di misura fondamentali in fisica: tempo, lunghezza e massa

L'intervallo di tempo

Per misurare un intervallo di tempo si conta quante volte la durata di un fenomeno periodico si ripete tra l'inizio e la fine dell'intervallo.

Alcune unità di misura del tempo sono:

• il giorno, cioè il tempo che separa due successive culminazioni del Sole;
• la settimana, cioè il tempo che separa due fasi lunari consecutive; l'anno, cioè il tempo che impiega la Terra a percorrere un'orbita completa intorno al Sole.

L'unità di misura degli intervalli di tempo nel SI è il secondo (s).

Conversioni tra unità di tempo

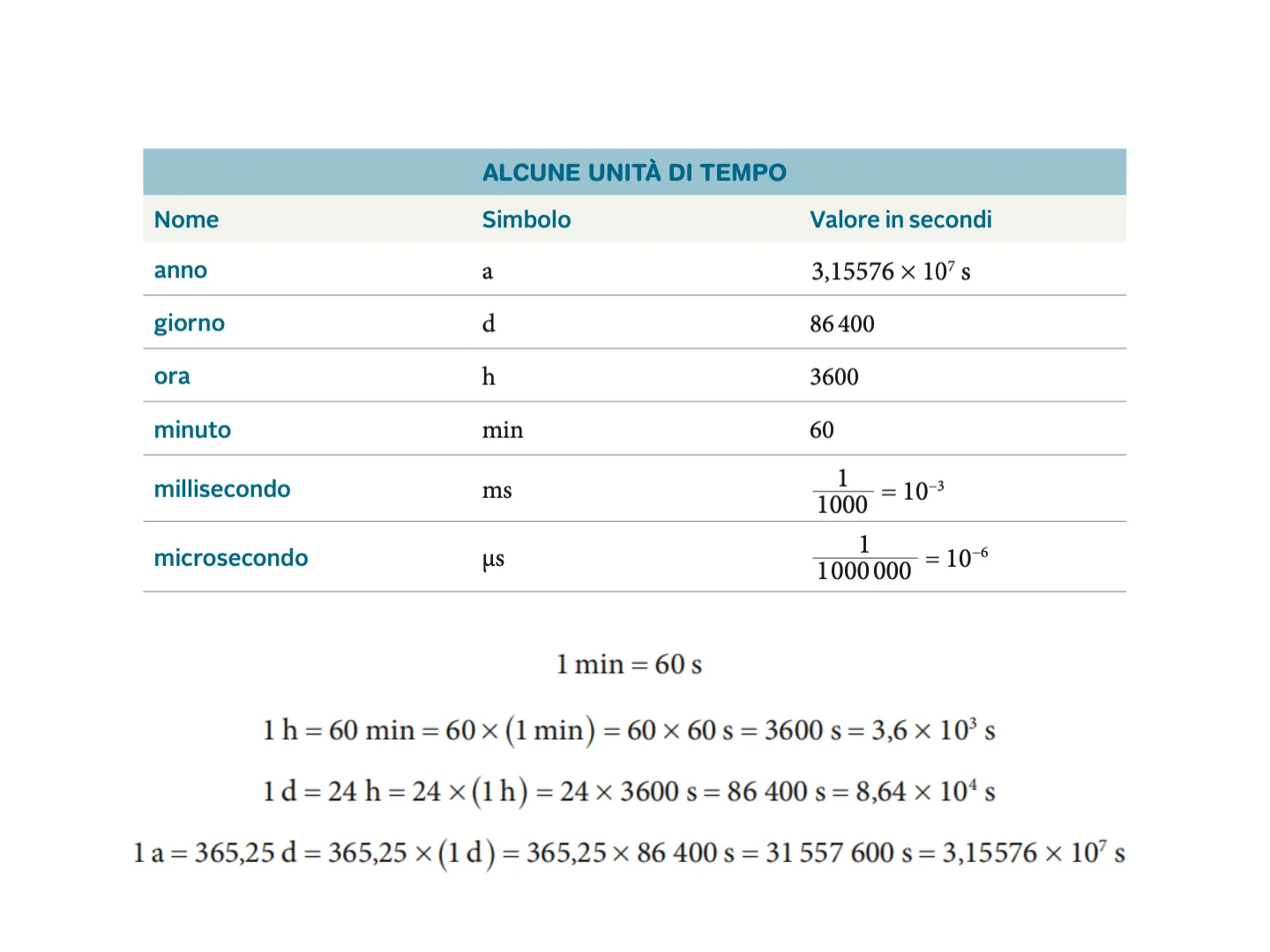
Alcune unità di tempo

Nome Simbolo Valore in secondi anno a 3,15576 × 107 s giorno d 86 400 ora h 3600 minuto min 60 millisecondo ms 1 = 10-3 1000 microsecondo με 1000 000

1 min = 60 s 1 h = 60 min =60x(1min) =60×60s=3600 s=3,6×103s 1 d = 24 h =24 x (1h) =24x 3600 s =86 400 s= 8,64x 104 s 1 a = 365,25 d = 365,25 x (1 d ) = 365,25 x 86 400 s = 31 557 600 s = 3,15576 x 107 s 1 = 10-6

La lunghezza

L'unità di misura della lunghezza nel SI è il metro (m). Il metro è definito come la distanza percorsa dalla luce nel vuoto in un intervallo di tempo di 1 299 792 458 S. Gli esperimenti mostrano che la velocità della luce nel vuoto, indicata con il simbolo c, non cambia nel tempo ed è uguale dappertutto. Il suo valore è fissato a: c = 299 792 458 m/s 12

Equivalenze con le unità di lunghezza

Oltre al metro sono usati anche multipli e sottomultipli di questa unità.

Multipli e sottomultipli del metro

Valore in metri kilometro (km) 1 km = 1000 m ettometro (hm) 1 hm = 100 m decametro (dam) 1 dam = 10 m 1 decimetro (dm) 1 dm = m 10 centimetro (cm) 1 cm = m millimetro (mm) 1 mm = 1000 m km :10 ×10 hm :10 x10 dam :10 ×10 m 10L :10 dm x10 cm :10 :10 ×10 mm 1 100 1

Esempio di conversione lunghezza

Esempio: 5,88 dm = 5,88 x 100 m = = 588 mm 13

La massa

La massa di un oggetto viene definita operativamente con una bilancia a bracci uguali. Due oggetti hanno la stessa massa se, messi ciascuno su un piatto della bilancia, questa resta in equilibrio, con i due piatti alla stessa altezza. oksana2010/Shutterstock L'unità di misura della massa nel SI è il kilogrammo (kg).

Equivalenze con le unità di massa

Oltre al kilogrammo sono usati anche multipli e sottomultipli di questa unità.

Alcune unità di massa

Valore in kilogrammi ettogrammo (hg) 1 hg 1 10 kg grammo 00 1 g = 1 1000 kg milligrammo (mg) 1 mg = 1000000 kg kg :10 10 hg x10 :10 dag :10 ×10 g :10 ×10 dg :10 ×10 cg :10 1 ×10 mg 214

Esempio di conversione massa

Esempio: 214 g = 1000 kg = 0,214 kg

Grandezze derivate

Nel SI l'intervallo di tempo, la lunghezza e la massa sono tre grandezze fisiche fondamentali; invece l'area e il volume sono grandezze derivate. Si chiamano grandezze derivate le grandezze fisiche che sono definite a partire dalle grandezze fondamentali. Le loro unità di misura si deducono da quelle delle grandezze fondamentali.

Il litro

Per esprimere il volume di liquidi e gas si usa spesso il litro (L), un'unità di misura che non fa parte del SI ma che è equivalente a un sottomultiplo del metro cubo. Un litro è equivalente a un decimetro cubo: 1 L = 1 dm3 Un litro contiene 1000 millilitri. D'altra parte, 1 dm3 contiene 1000 cm3. Quindi: un millilitro è uguale a un centimetro cubo: 1 mL = 1 cm3.

La densità

la massa di 1 L di latte è maggiore della massa di 1 L d'olio stesso volume (1 L) Massimiliano Trevisan La densità (d) di una sostanza è il rapporto tra la massa m e il volume V di un campione di quella sostanza: densità (kg/m3) massa (kg) d = m V volume (m3) continua

Definizione e unità di misura della densità

La densità densità (kg/m3) massa (kg) d = m V volume (m3) · Fissato il volume, la densità è direttamente proporzionale alla massa. · Fissata la massa, la densità è inversamente proporzionale al volume. L'unità di misura della densità è il kilogrammo al metro cubo (kg/m3), rapporto tra l'unità di massa e l'unità di volume.

Tabella densità di sostanze

Sostanza (o miscuglio) Densità (kg/m3) Platino 21 450 Oro 19 300 Mercurio 13 550 Argento 10 500 Rame 8960 Ferro 7860 La Terra 5515 Alluminio 2700 Il Sole 1410 Glicerina 1260 Il corpo umano 1070 Acqua distillata 1000 (a 4 ℃) Olio di oliva (a 20 ℃) 920 Ghiaccio 917 Aria (al livello del mare) 1,29 Aria (a 20 km di altitudine) 0,09

Formule inverse della densità

Formule inverse: la massa e il volume dalla formula della densità Se conosciamo la densità d di un materiale e il volume V di un corpo fatto di quel materiale, è possibile ricavare la massa m del corpo: dV= m -y => m = dV Se conosciamo la densità d di un materiale e la massa m di un corpo fatto di quel materiale, è possibile ricavare il volume V: m d dv = V= m d

Conversioni tra unità di densità

A volte la densità è espressa in g/cm3 invece che in kg/cm3. Per passare da g/cm3 a kg/cm3 si moltiplica per 1000; per passare da kg/cm3 a g/cm3 si divide per 1000.

Esempio di conversione densità

Esempio: Consideriamo la densità del ghiaccio, il cui valore è 0,917 g/cm3. 0,917 g 3 = 0,917 cm -6 10 ° m3 -3 103 kg m =9,17×103 kg m m 3 3 =917 kg