Le Funzioni Matematiche: Relazioni, Proprietà e Tipologie

Le Funzioni

Introduzione generale e sintesi delle dispense Partiamo con il concetto più generale di relazione, per passare poi a quello più funzione fra insiemi e, infine, riprendiamo il tema delle funzioni reali di variabile reale visto durante le scuole superiori

Relazioni fra due insiemi

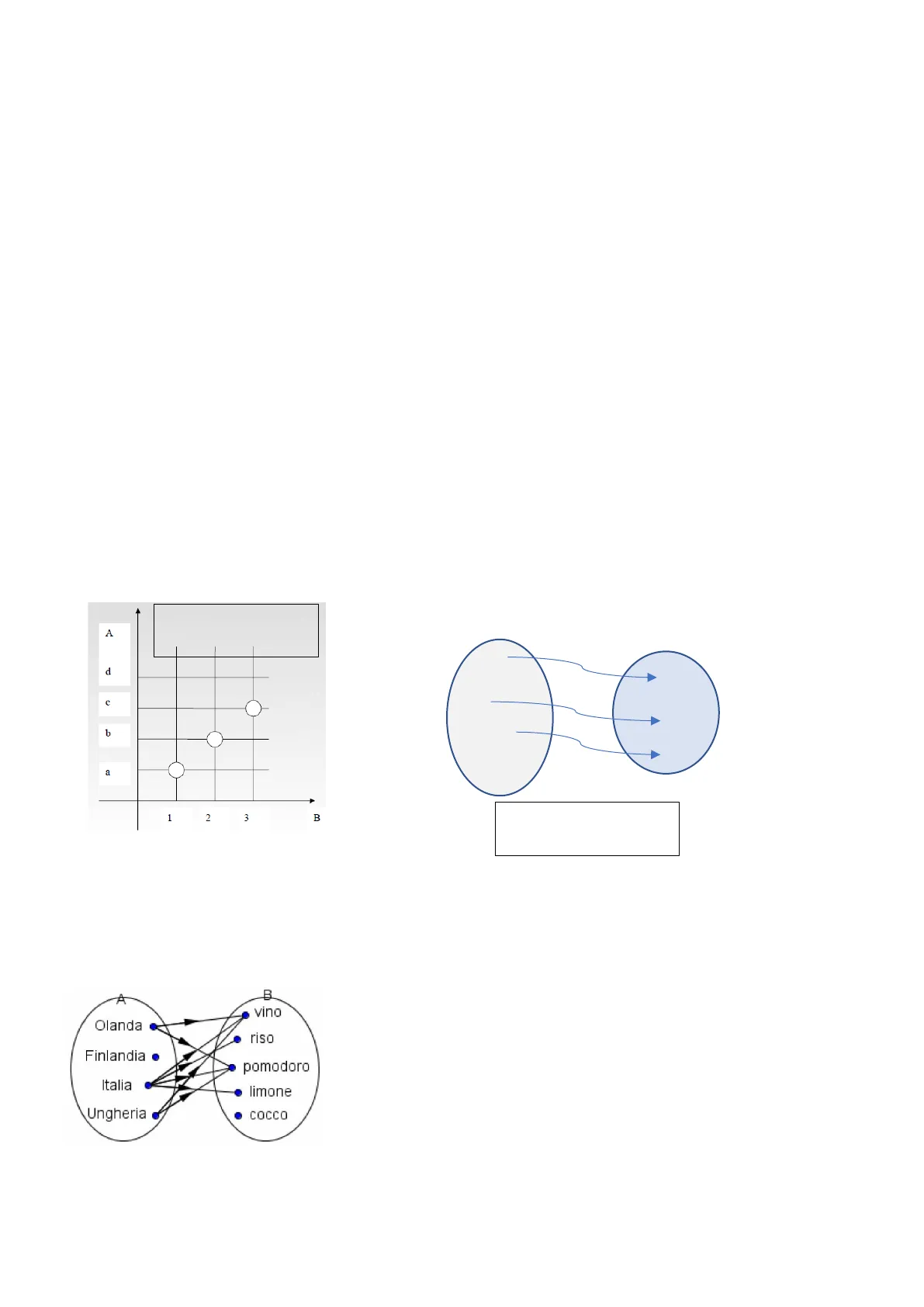
Si definisce RELAZIONE tra due insiemi A e B, e si indica spesso con R un qualsiasi sottoinsieme del prodotto cartesiano A x B: R C A X B Se A = {a, b, c, d} , B = {1,2, 3} R = {(a, 1), (b, 2), (c, 3)} c A x B è una relazione fra A e B In particolare, vediamo che a è in relazione con 1, b con 2 e c con 3, questo si scrive: aR1, bR2, CR3 La relazione può essere rappresentata in vari modi, ad esempio:

A Rappresentazione cartesiana d c b a 1 2 3 B a 1 b 2 C .3 d Rappresentazione sagittale

Altro esempio: A = {Olanda, Finlandia, Italia, Ungheria} e B = {vino, riso, pomodoro, limone, cocco} Se consideriamo la relazione definita dal predicato: " ... è nazione produttrice di ... " essa può essere rappresentata da

B vino Olanda · riso Finlandia pomodoro Italia · limone Ungheria · COCCO

quindi la relazione R è definita dal sottoinsieme:

G = (Olanda, Vino), (Olanda, pomodoro), (Italia, Vino) (Italia, Riso), (Italia, pomodoro), (Italia, limone) (Ungheria, riso), (Ungheria, pomodoro)

Da notare che Finlandia non è in relazione con nessuno dei prodotti in B e il cocco non è in relazione con nessuna delle nazioni in A. L'insieme G è definito anche come grafico della relazione RSempre considerando la generica coppia di elementi in relazione, che indichiamo con (a,b):

• b è chiamata immagine di a rispetto a R
• a è chiamata controimmagine di b rispetto a R
• l'insieme degli elementi immagine è chiamata codominio di R nell'esempio di prima: codominio = {vino, riso, pomodoro, limone}
• l'insieme degli elementi contro-immagine è chiamata dominio di R nell'esempio di prima: dominio = {Olanda, Italia, Ungheria}

Relazione interna

Una relazione fra un insieme A e sé stesso viene chiamata relazione interna Può essere rappresentata in forma sagittale duplicando l'insieme A oppure, più correttamente, in forma di grafo interno ad A, spieghiamo con un esempio A = {1,2,4, 6, 8, 10, 12} e consideriamo la seguente relazione R: 1R2, 2R4, 4R8, 6R12 Il suo grafo è a fianco Una relazione interna ad un insieme A può avere svariate proprietà:

• Proprietà riflessiva: aRa Va E A fig. a
• Proprietà antiriflessiva: Aa E A | aRa fig. b
• Proprietà simmetrica: aRb -> bRa Va, b E A fig. c È rappresentata nel grafo con un arco senza freccia
• Proprietà antisimmetrica: se aRb A bRa -> a = b Va, b E A fig. d Significa che vale la proprietà simmetrica esclusivamente quando a=b
• Proprietà transitiva: se aRb A bRc -> aRc Va, b, c E A fig. e

Nella rappresentazione con un grafo, le proprietà delle relazioni sono facil- mente individuabili: in una relazione riflessiva ogni elemento ha un anello, in una antiriflessiva nessun elemento ha un anello, in una simmetrica le cop- pie di elementi in relazione sono uniti da un arco doppiamente orientato, in una antisimmetrica non ci sono archi doppiamente orientati, in una transiti- va non ci devono essere situazioni "triangolari" non chiuse.

A 2 1. 10 4 8 12 6 . a. riflessiva b. antiriflessiva c. simmetrica d. antisimmetrica e. transitivaUna relazione che è riflessiva, simmetrica e transitiva si dice relazione di equivalenza. Le relazioni di equivalenza suddividono l'insieme A in sottoinsiemi detti classi di equivalenza, ciascuna delle quali contiene gli elementi di A che sono in relazione fra loro. L'insieme i cui elementi sono le classi di equivalenza si chiama insieme quoziente. Una relazione che è antisimmetrica e transitiva si dice relazione d'ordine; se vale anche la proprietà riflessiva la relazione è di ordine largo. Se due qualsiasi elementi di A sono sempre confrontabili rispetto alla rela- zione ØR, si parla di relazione d'ordine totale e si dice che A è totalmente ordinato. Se invece esistono almeno due elementi che non sono confrontabili la relazione d'ordine è parziale e l'insieme A si dice parzialmente ordinato.

Funzione

Una relazione fra due insiemi A e B è una funzione o applicazione di A in B se ad ogni elemento del primo insieme fa corrispondere uno ed un solo elemento del secondo; in questo caso, si parla anche di corrispondenza univoca fra A e B. Una funzione f fra l'insieme A e l'insieme B si indica in uno dei seguenti modi: f : A ->B Se poi A e B sono insiemi numerici e se la relazione che lega x e y si può esprimere mediante un'equazione, si scrive y =f(x) con x€ A Ay EB In base al tipo di legame che esiste fra gli elementi x e gli elementi y una funzione f si dice:

• suriettiva se l'insieme delle immagini coincide con l'insieme B (figura 6)
• iniettiva se ad elementi distinti di A corrispondono elementi distinti di B (figura 7)
• biiettiva se è contemporaneamente iniettiva e suriettiva (figura 8). In pratica, una funzione è biiettiva se ad ogni elemento di A corrisponde un solo elemento di B e viceversa; le funzioni biiettive si dicono anche cor- rispondenze biunivoche. Le funzioni biiettive sono le sole funzioni invertibili, tali cioè che la relazio- ne inversa f-1 sia ancora una funzione.

Figura 6 A B Funzione suriettiva Figura 7 A B Funzione iniettivaData una funzione f : A -> B ed indicato con B* l'insieme delle immagini, sia g la funzione che agli elementi di B* associa gli elementi di un altro insieme C (figura 9). Si può pensare alla funzione k che associa diretta- mente gli elementi x di A agli elementi z di C che provengono da un y di B *; questa funzione è il prodotto delle funzioni f e g e si scrive k = g of . Nella scrittura del prodotto, la funzione che viene applicata per ultima è indicata per prima.

Figura 9 A B C f B* g X y A Z gof

Funzioni analitiche in una sola variabile

Possiamo qui riepilogare le principali caratteristiche delle funzioni analitiche più comuni, viste anche durante le scuole superiori, che hanno una sola variabile indipendente Funzioni analitiche sono quelle in cui la relazione è fornita da un'espressione analitica, come siamo già abituati a vedere: y = f (x)La classificazione delle funzioni Le funzioni esprimibili analiticamente possono essere distinte in funzioni algebri- che e funzioni trascendenti. La funzione è algebrica se l'espressione analitica y = f(x) che la descrive contiene soltanto, nella variabile x, operazioni di addizione, sottrazione, moltiplicazione, divisione, elevamento a potenza o estrazione di radice. Una funzione algebrica può essere:

• razionale intera (o polinomiale) se è espressa mediante un polinomio; in par- ticolare se il polinomio è di primo grado rispetto alla variabile x, la funzione si dice lineare; se il polinomio in x è di secondo grado, la funzione è detta qua- dratica;
• razionale fratta se è espressa me- diante quozienti di polinomi;
• irrazionale se la variabile indipenden- te x compare sotto il segno di radice.

Se una funzione non è algebrica, si dice trascendente.

FUNZIONI algebriche trascendenti y = e", y = sen x razionali irrazionali y =\x+ 1 intere fratte 2x - 1 y = 5x - 7 y = 3x + 2

Per una funzione algebrica viene definito il grado della funzione, che è il grado del polinomio P(x; y), in x e y, che compare nell'espressione analitica in forma impli- cita della funzione P(x; y) = 0.

Il dominio di una funzione

e lo studio del segno

Spesso di una funzione si considera come dominio il sottoinsieme più ampio di R in cui la funzione può essere definita. In questo caso si parla di dominio naturale o campo di esistenza della funzione.

ESEMPIO La funzione y = Vx2 - 4 ha come dominio naturale l'insieme dei valori x per i quali il radicando del- l'espressione a secondo membro è positivo o nullo, ossia x ≤- 2 V x ≥2. Scriviamo sinteticamente: D: x ≤-2V x≥2.

Domini delle principali funzioni

Funzione Dominio naturale

Funzioni razionali intere: y = a0.x" + a1 x"-1 + ... + an R

Funzioni razionali fratte: y = P(x) Q(x) (P e Q polinomi) R esclusi i valori che annullano Q(x)

Funzioni irrazionali: y= \f(x) {xER| f(x) ≥0}, se n è pari dominio di f(x), se n è dispari

Funzioni logaritmiche: y = loga f(x) a > 0, a # 1 {xER| f(x) > 0}

Funzioni esponenziali: y = af(x) a> 0,a+ 1 dominio di f(x)

Funzioni goniometriche: y = senx, y = cosx y = tg x y = cotg x y = arcsen x, y = arccos x y = arctg x, y = arccotg x R R-{2 + KK} 12 R - {km} [-1;1] R·

I grafici di alcune funzioni

La funzione lineare

yt y = mx + q q TO x 8 .... m = tgo

La funzione esponenziale

yÎ y y = ax (a>1) y = ax (0 < a < 1) O X x

La funzione seno

y y = sen x 0 x

La funzione tangente

y y = tg x π 2 π 2 3 x

La funzione quadratica

y ¡y = ax2 + bx + c Ic V (- 2a- b. _ b2 - 4ac) 4a O

La funzione logaritmica

y y = log_x (a >1) y y = log_x (0

La funzione coseno

y y = cos x 2π x

La funzione cotangente

y = cotg x ... y O π 3 x π 2 2 -... ...

Le traslazioni

y y = f(x - a) ... P a O y = f(x) a. Traslazione di vettore parallelo all'asse x.

y P y = f(x) + b ... b .... P O x y = f(x) b. Traslazione di vettore parallelo all'asse y.

y V b y = f(x - a) + b a O y= f(x) c. Traslazione di vettore v(a; b).

Le simmetrie

y P X y= f(x) O x y =- f(x) P' a. Simmetria rispetto all'asse x.

y y = f(-x) .. X ....... P y = f(x) O x y =- f(-x) c. Simmetria centrale rispetto a O.

y y = f ( x) 1 y = f(x)' d. Simmetria rispetto all'asse x delle parti del grafico di y = f(x), con y < 0.

y y= f( x ) y = f(x) e. Per x ≥ 0 il grafico è lo stesso di y = f(x), per x < 0 il grafico è il simmetrico rispetto all'asse y di quello che y = f(x) ha per x >0.

Le dilatazioni

y m > 1 y = f( X) x ..... y = f(x) a. Dilatazione orizzontale.

m < 1 y = f( X x O y = f(x) --- b. Contrazione orizzontale.

y n > 1 y n< 1 y=f(x) y = nf(x) .... d. Contrazione verticale. c. Dilatazione verticale.

y + P y = f(x) O x ... x y = nf(x) y = f(x) b. Simmetria rispetto all'asse y. P x ......

Proprietà delle funzioni analitiche

Le funzioni crescenti, le funzioni decrescenti, le funzioni monotone

DEFINIZIONE Funzione crescente Una funzione y = f(x) di dominio DER si dice crescente in senso stretto in un intervallo I, sottoinsie- me di D, se comunque scelti x1 e x2 appartenenti a I, con x1 < x2, risulta f(x1)

ESEMPIO La funzione y = x2 - 4 è crescente nell'intervallo I = [0; + %[. y y = x2 - 4 -2 O 2 x D= [0; +00[ -4 4 Figura 4 Un esempio di funzione crescente per x ≥ 0. Se nella definizione precedente sostituiamo la relazione f(x1)

ESEMPIO La funzione y= f(x) ={1 x x-2 se x ≤ 1 se 1

y y = 1 y = x - 2 1- 1 3 x y = I = ]-00; +00[ = R