Corso di Fisica: Tipi di grandezze fisiche, scalari e vettoriali

Corso di Fisica

Tipi di grandezze fisiche

P. Cortese Corso di Laurea in Scienze Biologiche a.a. 2023/2024

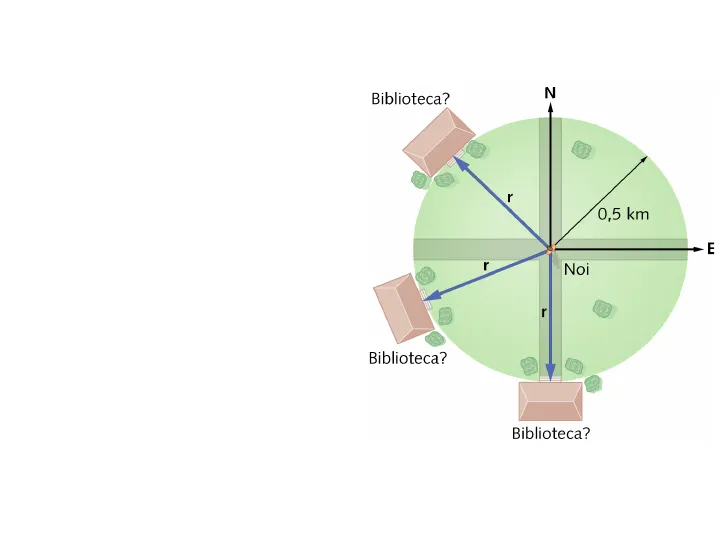
UP UNIVERSITÀ DEL PIEMONTE ORIENTALEDov'è la biblioteca? Aldo Scusi dov'è la biblioteca Giovanni Sarà a mezzo chilometro di distanza ... Aldo In che direzione? Giovanni Ma questo è proprio pignolo!

N Biblioteca? A r 0,5 km - E r Noi r Biblioteca? Biblioteca?

Grandezze scalari e vettoriali

Grandezze scalari

• grandezza scalare: si può specificare completamente utilizzando
• un numero (intensità)
• un'unità di misura
• un'incertezza

Esempi di grandezze scalari: la temperatura, il volume, la massa, gli intervalli di tempo, la distanza percorsa Per manipolare le grandezze scalari si usano le regole dell'aritmetica

988 980 976 1016 984 -996 -992 ~1008- -1000 1012- A A 1024 1020 -1024 1016 1012 A B B 1016 ºF 120 50 40 100 30 80 20 60 10 40 h min sec 1/100 0 20 -10 0 -20 74ºF

Grandezze scalari e vettoriali: introduzione

3/39 E V

1020 B 1004 1028 1016 SPLIT/RESET START/STOP 0.00.0000

Grandezze vettoriali

• grandezza vettoriale: oltre all'intensità (modulo) devono essere specificate anche:
• direzione
• verso

Esempi di grandezze vettoriali: la forza, lo spostamento Per manipolare le grandezze vettoriali bisogna anche tener conto di direzione e verso C'è un po' di ambiguità sul concetto di direzione. Infatti di solito specificando una direzione nello spazio (sono necessari due angoli) viene implicitamente specificato anche il verso ... Sarebbe più appropriato usare la parola "orientazione" al posto di "direzione", tuttavia per orientazione di un vettore si intende comunemente il verso ... @

Grandezze scalari e vettoriali: vettori

4/39 VI vettori: definizioni

• Modulo (intensità) di un vettore v
• Versore: un vettore unitario (per cui v = 1)

Esempi: i, j, k sono tre versori diretti verso la direzione positiva degli assi x, y e z rispettivamente Due vettori v1 e v2 sono uguali se sono identici: · modulo · direzione · verso

Grandezze scalari e vettoriali - I vettori

5/39 VModulo

N Biblioteca? 4 r 0,5 km Modulo: 0.5 km E r Noi r Biblioteca? Biblioteca?

Grandezze scalari e vettoriali - I vettori: modulo

6/39 =Direzione

N Biblioteca? I 4 I 0,5 km - E Noi r - I Direzione: verticale Biblioteca?

Grandezze scalari e vettoriali - I vettori: direzione

7/39 VVerso

N Biblioteca? 4 r 0,5 km E r Noi r Verso: Sud Biblioteca?

Grandezze scalari e vettoriali - I vettori: verso

8/39 VVettore posizione e sistemi di riferimento

• Per descrivere una grandezza fisica di tipo vettoriale come la posizione di un punto nello spazio occorre specificare un sistema di riferimento Esiste un sistema di riferimento privilegiato che possiamo scegliere come "centro dell'universo" per poter fare le misure e studiare correttamente le leggi della fisica?
• Non esiste, tuttavia non è necessario
• È sufficiente capire come collegare le osservazioni fatte in sistemi di riferimento diversi.
• È opportuno scegliere un sistema di riferimento adatto al problema che si considera (è il sistema di riferimento nel quale le formule sono più semplici).

Grandezze scalari e vettoriali - I vettori: posizione

9/39 VUn vettore

via Marconi N Biblioteca ---- Vertice -E via Fermi via Galileo r - via Copernico Noi ello Origine eucci Componenti (o punto di via Via via applicazione) corvo

Grandezze scalari e vettoriali - I vettori: componenti

10/39 E V r = 1 x y ) via Giorgione via Tizian via Michelangelo

Caso bidimensionale: componenti di un vettore

Si possono specificare: · le due componenti lungo l'asse x e y del vettore · l'angolo 0 e la lunghezza del vettore (distanza del punto P dall'origine) Per passare da coordinate polari a coordinate cartesiane: · dx = d cos 0 · dy = d sin 0 L'operazione inversa porta ad avere d = d2 + d3 0 = arctan dy dx I segni permettono di capire in quale quadrante si trova il vettore

y P dy 7 d sin 2 -> d To I x dcosa ? dx ả = 1 dx dy )=( cos e sin 0 d cos 0 d sin ℮ ) =al 1

Grandezze scalari e vettoriali - I vettori: caso bidimensionale

11/39 E

Convenzione sui nomi dei vettori

y b V ab a O Si utilizza una convenzione per il nome dei vettori per cui nella scrittura Vab · il primo indice a indica l'origine · il secondo indice b indica il vertice X

Grandezze scalari e vettoriali - I vettori: convenzione

12/39 E VVettore posizione: componenti nello spazio

Per specificare la posizione di un punto nello spazio abbiamo bisogno di: · un sistema di riferimento · tre informazioni indipendenti (spazio tridimensionale) · coordinate cartesiane · distanza dall'origine e due angoli che specificano la direzione (e allo stesso tempo il verso, per cui spesso si parla solo di "direzione")

2 z di - P θ d 1 d Y ol - ϕ - ---. y x Attenzione alle diverse convenzioni usate La convenzione degli angoli usata in fisica considera l'angolo 0 a partire dall'asse z e quindi compreso tra 0 e T.

Grandezze scalari e vettoriali - I vettori: componenti nello spazio

13/39 V

Conversione tra coordinate sferiche e coordinate cartesiane

x = d sin e cos y y = d sin 0 sin y z = d cos 0 d = d dz dx = d sin e cos y d sin 0 sin y d cos 0 - 1= = d sin e cos y sin e sin o cos e z die - 1 P d.cos 2 θ d d.sin@.since 1 1 1 0 X -- - - y o. sin 2 x

Grandezze scalari e vettoriali - I vettori: coordinate sferiche

14/39 V E disinO.cos q dy ϕ

Operazioni sui vettori

1. Somma
2. Differenza
3. Prodotto
   • Prodotto di uno scalare per un vettore
   • Prodotto scalare
   • Prodotto vettoriale

Grandezze scalari e vettoriali - Operazioni sui vettori

15/39 VSignificato della somma di due vettori

y b c 10 x Si considera l'effetto di due fenomeni che hanno caratteristiche vettoriali, ad esempio due spostamenti consecutivi · primo spostamento rappresentato da a · secondo spostamento rappresentato da b · lo spostamento risultante è rappresentato da c Per ottenere il risultato si può utilizzare il metodo "coda-punta"

Grandezze scalari e vettoriali - Somma di vettori

16/39 VSomma di vettori

Valgono le consuete proprietà della somma. Ad esempio è commutativa.

y y à 1 1 1 1 1 1 c c 1 1 b 1 1 / 10 x x In tutte le rappresentazioni dei vettori il risultato è la diagonale del parallelogramma formato da a e b

y - 1 1 1 1 1 - 11 C 15 x č = a + b Per ottenere il modulo della somma si applica la regola del parallelogramma c2 = a2 + b2 + 2ab cos 0

Grandezze scalari e vettoriali - Somma di vettori: proprietà

17/39 V 1 - b /A 1

Somma: casi particolari

b č à č Per due vettori paralleli e = 0 c2 = a2 + b2 + 2ab cos 0 => a2 +b2 +2ab = (a+b)2 c = a + b Per due vettori antiparalleli 0 = TT c2 = a2 + b2 + 2ab cos 0 => a2 + b2 - 2ab = (a -b)2 c = a - b

y b 10 10 x Per due vettori perpendicolari 0 = TT /2 c2 = a2 + b2 + 2ab cos 0 => a2 + b2 c = Va + b teorema di Pitagora

Grandezze scalari e vettoriali - Somma di vettori: casi particolari

18/39 V ESomma di vettori: effetto sulle componenti

y 1 by b cy V C 1 ay x a dx > - Cx - Le componenti vengono sommate Per i vettori valgono quindi tutte le proprietà dell'addizione tra numeri · a + b = b + à · d + (b +c) = (a + b)+č · esiste Ở per cui a + 0 = a · esiste b tale che a + b = 0

Grandezze scalari e vettoriali - Somma di vettori: componenti

19/39 V E Cx bx Cy ( č = a + b )=(ax ) +( b) by )=( ax +bx ay + by ) [Cx= Cy = ay +by ax +bx

L'opposto di un vettore

y B -B L'opposto di un vettore ha: · stesso modulo · stessa direzione · verso opposto Le componenti vengono cambiate di segno -b =- ( bx by )=( -bx -by ) x

Grandezze scalari e vettoriali - Differenza di vettori

20/39 VLa somma di vettori opposti è pari a zero!

Questo è spesso visibile in fenomeni fisici e naturali Velocità uguali ed opposte Velocità uguali ed opposte Forze uguali ed opposte equilibrio >

Grandezze scalari e vettoriali - Differenza di vettori: somma di opposti

21/39 VDifferenza di vettori

y T 1 1 1 1 / 1 b 10 x a La lunghezza del vettore differenza di due vettori è data dall'altra diagonale del parallelogramma č = a - b c2 = a2 + b2 - 2ab cos 0 (gener. del t. di Pitagora) · a con il segno + indica la testa del vettore · b con il segno - indica la coda del vettore

y y T 1 1 1 1 C - b /A 1 / x a 1 / − b č 1 č = à - b = å + (-b) Il vettore b - a ha la stessa lunghezza ma è diretto nel verso opposto rispetto ad a - b

Grandezze scalari e vettoriali - Differenza di vettori: lunghezza

22/39 V E − 10 1 b θ a x -č = b-à

Differenza di vettori: effetto sulle componenti

č = à - b {cx= ax-bx Cy = dy +by ( Cx Cy )=( ay ax )-( b;)=( ax - bx ay - by y C 1 b/Q 1 a x - Cx aux Le componenti vengono sottratte

Grandezze scalari e vettoriali - Differenza di vettori: componenti

23/39 V E

Prodotto di un vettore per uno scalare

Dato un vettore a e uno scalare m il risultato è un vettore: b = mã tale che abbia: · Modulo: b = |m| |a| · Direzione uguale ad a · Verso: · uguale ad a se m > 0 · opposto se m < 0 b = 2a č = - 3ã Un esempio è la seconda legge di Newton F = må Le componenti del vettore vengono moltiplicate: bx =m .ax by = m . dy bz = m . az vale anche la proprietà distributiva: m (a + b) = må + mb

Grandezze scalari e vettoriali - Prodotto di vettore per scalare

24/39 E

Prodotto scalare

à Dati due vettori a e b viene definito prodotto scalare: c = à · b = ab cos 0 dove 0 è l'angolo compreso tra i due vettori Il prodotto scalare è uno scalare Valgono le proprietà: · commutativa: a · b = b · à · distributiva: a · (b +c) = a · b +à · č

Grandezze scalari e vettoriali - Prodotto scalare: definizione

25/39 V

Importanza in fisica

Proiezione di à su b 1 𝑏 b à 1 1 1 b à 1 0 Proiezione di b su a Il prodotto scalare dipende dalla colinearità di due vettori: c = à · b = ab cos 0 · a cos 0 è la componente di a nella direzione di b · b cos 0 è la componente di b nella direzione di a Utilizzato nella definizione del lavoro di una forza. Si valuta l'effetto della forza: se c'è un'accelerazione collineare con la direzione del moto e quindi se la forza sta aumentando o diminuendo il modulo della velocità.

dr P F θ Se due vettori sono perpendicolari allora: 0 = = = > a . b = 0 ma non vale il viceversa perchè la condizione potrebbe anche essere verificata se a = 0 oppure b = 0

Grandezze scalari e vettoriali - Prodotto scalare: fisica

26/39 V

Prodotto scalare in termini delle componenti

Si esprimono i vettori in termini delle loro componenti: à · b = (axÎ+ dyj + azk · (bxÎ+byj+bzk)= quindi si applica la proprietà distributiva e si vede che tutti i termini misti sono nulli perchè i tre versori unitari sono perpendicolari tra di loro: a . b= axbxî·î+aybyj·ĵ+azbzk ·k+ +axbyl · j + axbzî · k + ... (altri termini misti) = axbx + dyby + azbz · Può essere utilizzato per calcolare il modulo di un vettore [a] = Va'2 + a2 + 2 = Vã · ã · Può essere utilizzato per stabilire se due vettori sono perpendicolari

Grandezze scalari e vettoriali - Prodotto scalare: componenti

27/39 V E