Algebra: introduzione a monomi e operazioni fondamentali

ALGEBRA

Monomio

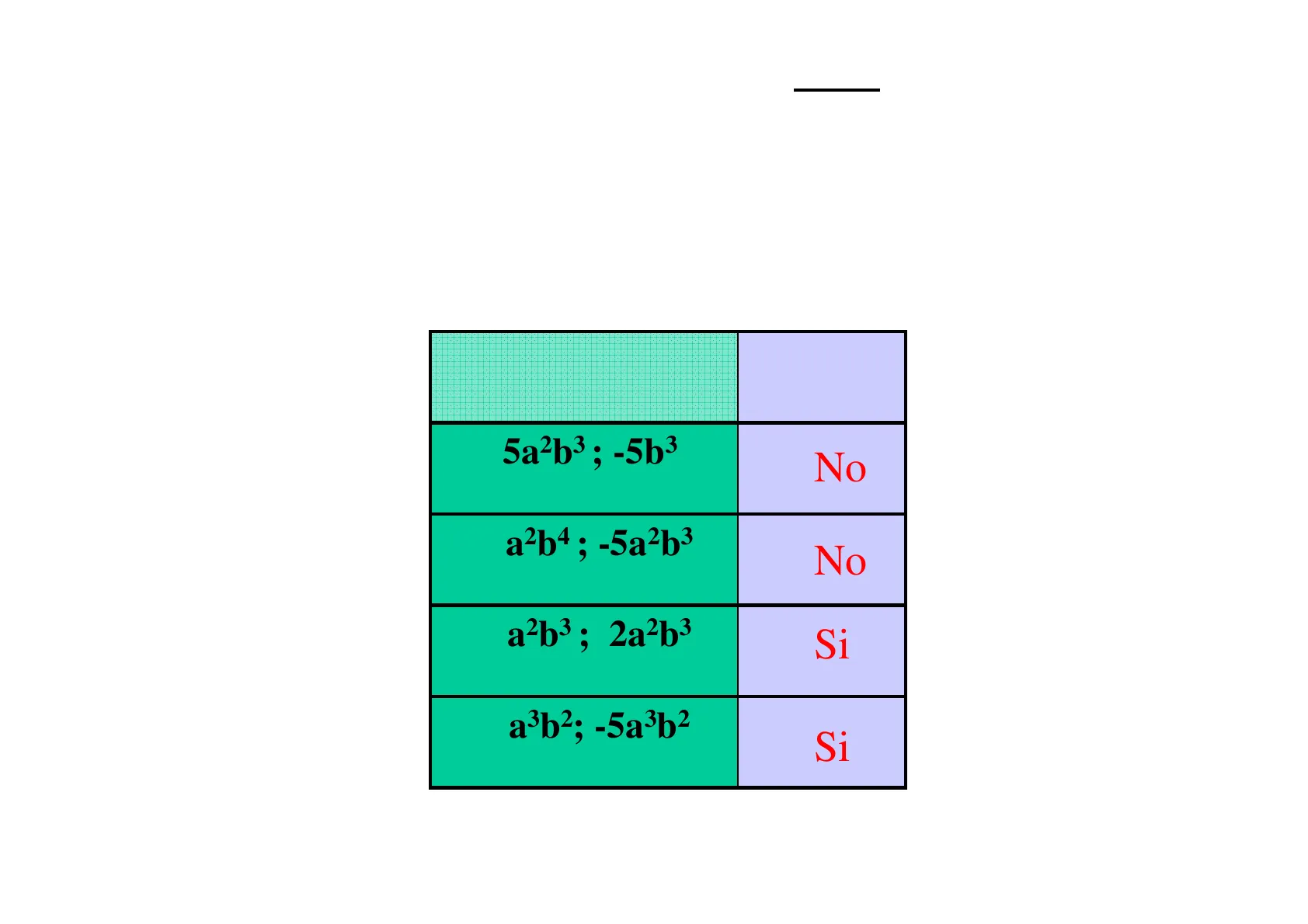
Monomio: un'espressione algebrica dove non figurano operazioni (e non segni) di addizione (+) o sottrazione(-); figurano solo moltiplicazioni e potenze. In un monomio distinguiamo parte numerica (o coefficiente) e parte letterale. Es .: - 7 ax2b3y coefficiente Parte letterale Es .: - 5a2b3 SI Es .: - 5a2b3+2 NOMonomi simili: due o più monomi sono simili quando hanno la stessa parte letterale (compresi gli esponenti) In pratica i monomi simili differiscono solo per il coefficiente

Monomi Simili

Monomi -5a2b3; - 563 No PERCHÉ LE LETTERE SONO DIVERSE -8a2b4; - 5a2b3 No -6a2b3; 2a2b3 Si -7a3b3; - 5a3b2 Si sirieOperazioni sui monomi

Addizione di Monomi

Addizione: v la somma tra monomi si può effettuare solo se i monomi sono simili, Cioè hamo STESSA PARTE LETTERALE v in tal caso basta sommare i coefficienti e riscrivere la stessa parte letterale. 1º monomio : 2° monomio -5a2b3+ 363: non si può effettuare Parte letterale Parte letterale coefficiente coefficiente Somma dei coefficienti -5 b3 +3 b3= -2 63 La parte letterale si riscriveProdotto: il prodotto tra monomi si può effettuare sempre:

Prodotto di Monomi

v basta moltiplicare i coefficienti e le parti letterali V .(le lettere comuni si riscrivono sommando gli esponenti, quelle non comuni si riscrivono inalterate) Sempre SI f 1º monomio 2º monomio Le lettere non comuni si riscrivono inalterate Anol -5a2b3 . 3b3= - 15a2b6 le lettere comuni si riscrivono sommando gli esponenti fore Parte letterale Parte letterale coefficiente Prodotto delle parti letterali coefficiente Prodotto dei coefficientiQuoziente: il quoziente tra monomi si può effettuare sempre:

Quoziente di Monomi

v basta fare il quoziente dei coefficienti e delle parti letterali v (le lettere comuni si riscrivono sottraendo gli esponenti, quelle non comuni si riscrivono inalterate) Le lettere non comuni si riscrivono inalterate 1º monomio 2º monomio le lettere comuni si riscrivono sottraendo gli esponenti -25a2b3c5x9y9 : 15b°c4x2= - 5/3 a2b-3cx7 y9 Parte letterale Parte letterale coefficiente coefficiente Quoziente dei coefficienti Quoziente delle parti letteraliPotenza:

Potenza di un Monomio

La potenza di un monomio si può effettuare sempre: v basta fare la potenza del coefficiente e della parte letterale v (la potenza della parte letterale si effettua facendo la potenza delle singole lettere, ossia moltiplicando i singoli esponenti) La potenza delle singole lettere si effettua moltiplicando gli esponenti Monomio base della potenza (-2a2b3c5x9y)6= 64 a12b18c30x54 y6 Parte letterale coefficiente Potenza del coefficiente Potenza della parte letteralePolinomio: È la somma algebrica di più monomi

Polinomio

I polinomi, in base al numero di monomi che li compongono vengono detti: binomi: a+b trinomi: a+b+c quadrinomi: a+b+c+d Es .: - 5a2b3 NO Es .: - 5a2b3+2 Si: è un binomioGrado di un polinomio:

Grado di un Polinomio

È dato dal grado massimo dei suoi monomi

Polinomio Omogeneo

Polinomio omogeneo: Quando tutti i suoi monomi hanno lo stesso grado

Polinomio Ordinato

Polinomio ordinato: Quando i suoi monomi figurano in ordine crescente (decrescente) di grado

Polinomio Completo

Polinomio completo: Quando i suoi monomi figurano con tutti i possibili gradi (dal massimo fino al grado zero) Polinomi -5a2b3+8xy+5b3 Grado 5 -8a2b4 -5a 3b 3+5a6 Omogeneo di grado 6 -6a4+a3 +a+1 Ordinato incompleto -7a2+a3 -5a+2 Completo non ordinato -6a4+a3+a2+a+1 Completo ordinatoOperazioni sui polinomi

Addizione di Polinomi

Addizione: v la somma tra polinomi si effettua sommando i monomi simili

Differenza di Polinomi

Differenza: v la differenza tra polinomi si effettua togliendo le parentesi, cambiando di segno tutti i monomi del secondo polinomio e quindi sommando i monomi simili. 1º polinomio 2º polinomio (-3a2-5a2b3-5ab3 -5b3) + (7a2b3-5ab3 +15a2+ 3b3)= =- 3a2-5a2b3-5ab3 -5b3 + 7a2b3-5ab3+15a2+ 3b3= =12a2+2a2b3-10ab3-2b3 1º polinomio 2º polinomio (-3a2-5a2b3-5ab3 -5b3) - (7a2b3-5ab3 +15a2 + 3b3)= =- 3a2-5a2b3-5ab3 -5b3 - 7a2b3+5ab3-15a2-3b3= =- 18a2+12a2b3-8b3Prodotto: Si moltiplica ciascun monomio del primo polinomio per tutti i monomi del secondo polinomio

Prodotto di Polinomi

v .(le lettere comuni si riscrivono sommando gli esponenti, quelle non comuni si riscrivono inalterate) (-5a2+b3) . (3x+3b3)= - 15a2x -15 a2 b3 +3x b3 +3b6Prodotti notevoli:

Somma per Differenza di Monomi Uguali

Somma per differenza di monomi uguali Si esegue facendo il quadrato del primo monomio meno il quadrato del secondo monomio (a+b) . (a-b)= a2 -ab +ab -b2 =a2-b2 (a+b) · (a-b)= a2-b2 la regola del prodotto tra polinomi è sempre valida, ma, come si può osservare nella dimostrazione accanto, i termini misti si elidono, per cui verrà ricordata la regola della somma per differenza di monomi uguali sopra enunciataProdotti notevoli:

Quadrato di un Binomio

Quadrato di un binomio Si esegue facendo il quadrato del primo monomio più il doppio prodotto del primo monomio per il secondo più il quadrato del secondo monomio (a+b)2=(a+b) . (a+b)= a2 +ab +ab +b2=a2+2ab +b2 (a+b)2= a2 +2ab +b2 v la regola del prodotto tra polinomi è sempre valida, ma, come si può osservare nella dimostrazione accanto, i termini misti si sommano, per cui verrà ricordata la regola del quadrato di un binomio sopra enunciataProdotti notevoli:

Cubo di un Binomio

Cubo di un binomio Si esegue facendo il cubo del primo monomio più il triplo prodotto del quadrato del primo monomio per il secondo più il triplo prodotto del primo monomio per il quadrato del secondo monomio più il cubo del secondo monomio (a+b)3=(a+b)2(a+b)= (a2+2ab +b2) . (a+b)= a3 +a2b+2a2b +2ab2 +ab2+b3= a3 +3a2b +3ab2 +b3 (a+b)3= a3 +3a2b + 3ab2 + b3 v la regola del prodotto tra polinomi è sempre valida, ma, come si può osservare nella dimostrazione accanto, i termini misti si sommano, per cui verrà ricordata la regola del quadrato di un binomio sopra enunciataProdotti notevoli:

Quadrato di un Trinomio

Quadrato di un trinomio Si esegue facendo il quadrato del primo monomio più il quadrato del secondo monomio più il quadrato del terzo monomio più il doppio prodotto del primo monomio per il secondo più il doppio prodotto del primo monomio per il terzo monomio più il doppio prodotto del secondo monomio per il terzo monomio, (a+b+c)2= (a+b +c). (a+b+c)= v la regola del prodotto tra polinomi è sempre valida, ma, come si può osservare nella dimostrazione accanto, i termini misti si sommano, per cui verrà ricordata la regola del quadrato di un trinomio sopra enunciata =a2+ab+ac+ab +b2 +bc +ac+bc+c2=a2+b2+c2+2ab+2ac+2bc (a+b+c)2= a2 +b2+c2+2ab+2ac+2bcSCOMPOSIZIONE IN FATTORI DI POLINOMI

Scomposizione in Fattori di Polinomi