Fisica 2: Campo e forza magnetica, moto particelle cariche

Campo magnetico

Forza magnetica

capitolo

6

10 SIMPLE MAGNET TRICKS!

Interazione magnetica, campo magnetico (par.6.1)

FeO, FezO

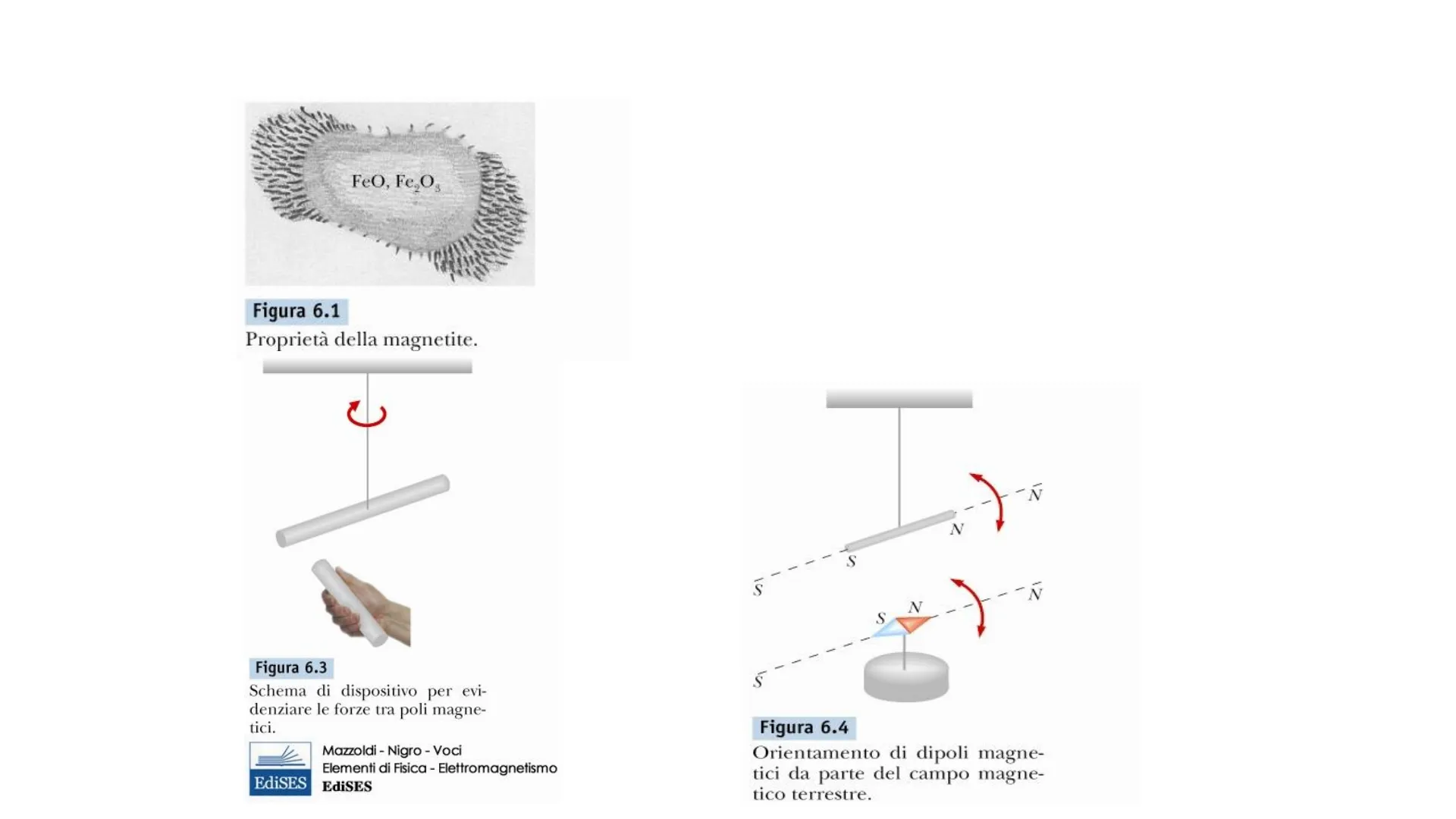
Figura 6.1

Proprietà della magnetite.

Alcuni minerali (es. magnetite) hanno la proprietà di attirare limatura di ferro o alcuni metalli (non tutti!) Tale proprietà si concentra in alcuni punti (POLI) I poli di due magneti si attraggono o respingono quando affacciati > esistono solo due tipi di poli

-Ñ N - 1 S 1 1 S 12 N S 1 1 1 1 1 Ś

Figura 6.3 Schema di dispositivo per evi- denziare le forze tra poli magne- tici.

EdiSES Mazzoldi - Nigro - Voci Elementi di Fisica - Elettromagnetismo EdiSES

Figura 6.4 Orientamento di dipoli magne- tici da parte del campo magne- tico terrestre.

Interazione magnetica, campo magnetico (par.6.1)

S N N S N S S N + -- Fd1

S N S N

Figura 6.5 Forze tra poli magnetici.

F&1 22

Per sbarrette lunghe e sottili con poli puntiformi la forza è proporzionale a 1/r2 (come per cariche puntiformi) Però non è possibile separare i due poli! La situazione è simile a quella di un isolante polarizzato > DIPOLI magnetici

N N N S S N S N N S S S

Figura 6.6 Esperienza della calamita spezza- ta.

T+ ++ ++ + + + + + - - conduttore + + - isolante

Interazione magnetica, campo magnetico (par.6.1)

Avvicinando un magnete ad un oggetto di ferro, quest'ultimo si magnetizza, cioè acquista proprietà magnetiche a sua volta, senza che il magnete ne risenta > Le proprietà magnetiche dell'oggetto restano anche se si allontana il magnete! > Diventa un magnete artificiale o calamita

S magnete N 5 S N N ferro ferro ferro

Questa persistenza delle proprietà non si verifica negli isolanti polarizzati!

Proprietà di un cilindro di magnetite

Figura 6.2 Proprietà di un cilindro di ma- gnetite.

Diremo che un dipolo magnetico crea un campo magnetico e si orienta in un campo magnetico esterno

B S N

Figura 6.7 Linee di un campo magnetico uniforme.

B = campo magnetico (o induzione magnetica) Le linee di campo sono determinate usando un piccolo ago magnetico

Visualizzazione delle linee del campo magnetico

Come visualizzare le linee del campo magnetico Come visualizzare le linee del campo magnetico (ferrofluid)

A B B x x X x (a) (b)

Figura 6.8 Convenzioni per la rappresentazione delle linee del campo magnetico B: (a) uscente dal foglio ·, (b) entrante nel foglio X.

N geografico S magnetico N N N magnetico S geografico

Figura 6.9 Linee del campo magnetico terrestre.

Elettricità e magnetismo (par.6.2)

1. Un filo percorso da corrente crea intorno a sé un campo magnetico che si può evidenziare con un ago magnetico o con limatura di ferro ...
2. Un filo percorso da corrente immerso in un campo magnetico subisce una forza

1 B

Figura 6.10 C F

1. Due fili percorsi da corrente si attraggono o respingono a seconda del verso delle correnti
2. Campi elettrici variabili nel tempo creano campi magnetici!

2 F F F

Figura 6.12

Interazioni magnetiche e cariche in moto

Le interazioni magnetiche non sono altro che la manifestazione dell'interazione tra cariche in moto !! Le proprietà magnetiche della materia sono dovute a correnti microscopiche (negli atomi o nelle molecole) che danno origine a momenti di dipolo magnetico Anche protoni, neutroni ed elettroni hanno un loro momento di dipolo magnetico L'elettrone ha un momento di dipolo magnetico, ma essendo puntiforme tale momento non può essere dovuto a correnti. > Momento di dipolo intrinseco (dovuto al momento angolare intrinseco o spin) I campi magnetici sono creati da cariche elettriche in moto

quark q= se q=je q =- te gluoni 10-15 m

Figura 6.13 L'interazione nucleare forte, la più intensa delle forze fonda- mentali della natura, trasmessa dai gluoni, permette ai quark di rimanere uniti tra loro nel pro- tone (neutrone).

Forza magnetica su una carica in moto (par.6.3)

AF / B B 0 0 9+ 9 0 F (a) (b)

Figura 6.14 Forza di Lorentz su una particella in moto con carica posi- tiva (a), con carica negativa (b).

carica ferme : non sente il compo magnetico codice in proto in un campo B con velocità " sente una forza magnetica forza di Lorenzo F= günB 1 col segno! il verso di È depende del segno di 9! le linee d' compo d'À non sono linee di forse! IS 2 ( dinero de É dove F // Æ ! ) F1 B

Magnetic Forces Demonstration - Penn Physics

Lavoro della forza magnetica

FIN F 1 de ! SW = F. de = 0 1 A 9H. B Je = vidt la forse magnetica non compie lavoro durante il moto delle cariche! WAB = B SF. de = 0 A (a) AF (b) F = qE B +q 0 +9 Q ds v dW = dE = F. ds = 0 W = AE, = - q (V2 - Vp)

Figura 6.15 non vore le velocità (in modulo) Il campo magnetico (a) las una particella carica, mentre il campo elettrostatico (b) la accelera.

EdiSES Mazzoldi - Nigro - Voci Elementi di Fisica - Elettromagnetismo EdiSES

È non può variare l'énergie cinetica > non varia il Modulo d' À En = = mv Pò il campo magnetico prò cambiare la direzione d' v°

9 Se È è l'unica fosse W = DEK = (En) B- (EK) A=0 AB

Unità di misura del campo magnetico

P.Unità di misura del campo magnetico F= 9 ~~ B 11 F 11= 19/ 5 B sind 9 B 12 IF/1= 0 se sino = 0 ciai se BIIV IFI & max quando sind =1 cioè B 1V [F] = [9] [v][ B] [B] = [F ] [9][ N] ] CMIls , - (N) = V. S = V.S del m2 V. s = Wb (weber) [B]= W} = T M2 1 Table = 1 Wb 1 V.S 1 m2 il compo terrestre è 4. 10° T 3 gaun [ non è del 5] 1 gaun = 1047

Moto di una particella carica in campo magnetico (par.6.7)

B uniforme, v perpendicolare a B

linee di comp rette e parallele - B KD 1 13 15 F F B +9 U F C

Figura 6.27 Moto di una carica in moto in un campo magnetico uniforme per- pendicolare al piano della traiet- toria.

F= gříše mã a = 95AB m Hall = qNB sim (1/2) è contante à è centupete! a = No? R 191NB Sin(Th)= ma = min2 1 EdiSES Mazzoldi - Nigro - Voci Elementi di Fisica - Elettromagnetismo EdiSES Nº 1 B = la forza è massima F = qüAB 15 B 9 NL

B uniforme, v perpendicolare a B (continuazione)

19/1/B = mv2 R w= = = mu N /a/B 191B M Trovo il vettore Tù 1 1 13 Scrivo qÑ & B = mã = m(wMv) - 9 BÃV = MŰav a = ünü Buscente 1 1 B K X X 15 -q -1 F > 3 X 3 × · 14 5 K x X 12 K X × × × 5 × 9>0 Vedere esempio 6.4 R = MV 191B raggio delle circonferenze il moto è circolare miforma Beninaute -9B=mw-/w =- 9B x 15 m +q +9 × X x x X F X X X × x 7 15 920

B uniforme, v perpendicolare a B (periodo e frequenza)

W = - 9B m R= MV 191B T= periodo della porazione = 217 w T = 2TIM = 2TR 191B f == (frequenza) f= 19/B 2TIM . × x × . +q +9 x × > 3 X 3 × . F X X × × 5 × 9>0 B K X 13 -q -9 F x x X 14 5 K x X 12 K X X 920 Vedere esempio 6.4 13 . X X 11 will = w = 19/ B

B uniforme, v forma un angolo 0 con B

v= Np Ms + NuMy = Np + Nn y 15€ X 7 B = BÂ+ Nn= N SiMO Np = N CON F= qÑAB = 9 (Np+Ñn) AB P B 2 Np 1 B , ÑpXÃ=0 3 q + U 1 U 0 - 0 R P 0 + B B le particelle descrive me circonferenza d' reggio Figura 6.29 Moto elicoidale di una particella con carica positiva in campo magnetico uniforme.

R= Mün = MNSiNO 191B 19 B Mazzoldi - Nigro - Voci Elementi di Fisica - Elettromagnetismo EdiSES 14 EdiSES = qÑp1B + günAB 7 F = qvà1B

B uniforme, v forma un angolo 0 con B (continuazione)

Poichè però Noto - la traiettoria è n'elica 1 P 1 P= NOT = N: 27M 191B P = 2TI MIN CON 19B P= 0PT = NO. 2TR = N CON 25. MV Sin Na N Simo 191B 27 mvcon 191B B B B B B, Z

Esempio di campo non uniforme: NOTA

Figura 6.30 15 BOTTIGLIA MAGNETICA E FASCE DI VAN ALLEN

p= passo dell'alice R= mUsing 19/B

Effetto Hall (par.6.6)

PPEffetto Hall (par.6.6) j = meño 7 X y B 15 se ero a eLo b + F Q 3 Z F = eNOMB e70 150 IL 5 B e Lo F 2 = ab e = carica dei portatori e>0 : lacune eco: elettroni No è nel verso di j id è nel verso apporto a F le cariche tendono a spostarsi lugo l'asse 7

Effetto Hall (par.6.6) - campo elettromotore

ero X B a ,1 13 x EH + P b 5 Q z F = evoAB E= 통 = 접 시 E1= campo elettromotore di Hall Se eso è diretto de P verso Q E4 = EN97 EL= EHM2 offene EM =- ENû1 L EH= ± ENÛ+ En é de Q verso P se eLo F = evon B nx eco y + a EN F P 1 b 5 Q z E= 통 =π へ En= En(-M+)= - EHÙ7

Effetto Hall (par.6.6) - tensione di Hall tra P e Q

ero X 1 1 a * * * * * P b J 2 z X eco Eel a En P b Q 5 Z EH= {"Eu de P E 4 = ± E .Î, (+ se ero - se eco) Eu= = |EMMz.DE = = EH d= = + EHb P Le cariche accumulate credo in comp entratico Éel All' quilesno Fel+1 =0 - Fe =- EH En = ± E+b = ("EH. dr =- JEQ.de = VQ-Vp P

Effetto Hall (par.6.6) - misurazione

ero X 1 a E P b + J 2 Z Perciò VQ - Vp = = Eub Mismando Va- Vp pero capire il segno dei portato. { Yq - Vo > O - eso VQ - VpLO - eLa 1 X eco + a EM P b Q J z

Effetto Hall (par.6.6) - calcolo di B o n

VQ- Vp = = EHb = EH | VQ- Vp) = Eu b = N Bb 1 = J Bb ne = i Bb M/elab IVQ- Vp 1 = i mela B da qui pero mismore B (se mi è noto) open n (se B è noto) semplicemente mismondo ma ddp En= = = CUIAB = BOMB 11 EAll= EH = Nd B a b J ' J = ' ab F = MeÑO J= m/C/Nd - VI = J M/el

Forza magnetica su un conduttore percorso da corrente (par.6.4)

TH B + 150 i F 0B dc = Eds 3 VI 7 1 Ids - J F= tevi AB F = - CTIAB la quantità di moto nel verso di F acquisita dai portatori the un muito e l'altro Nievre caduta al cristallo durante gli uni -> il cristallo subisce una forza melvero di F -> il conduttore subisce una farsa elemento di Nolme Edsada del conduttore la fase sukita per effetto del campo è dF = (- eÑanB) M dz = m(-e) Ñan B de = dz = Eds JABEds = TEds A B = JEd51B di vettore di madrelo ds nel Nero della comente dF = i d5A Ñ"

Forza magnetica su un conduttore percorso da corrente (par.6.4) - legge di Laplace

dF = i ds A B I legge elementare di Laplace AB ds dẾ 0 B Q ds di 1 층 La forse su un conduttore di emphera finita è F= JdF = {idJÃ P Se ha un circuito chiuso 2 V B di dù è nel vero delle corrente !

Forza magnetica su un conduttore percorso da corrente (par.6.4) - filo rettilineo

Filo rettilineo, campo uniforme B 9 ds Pás, 1 P F= fid518 = i(25) 1} P F = i POMB Il Pall=e 9 1 1 F = i enà P F = CAdeAB 11 P ids1 MB + id521 B + id5,1B i (dis1 + dj2 ... één) AB / ds = l 125=22

Forza magnetica su un conduttore percorso da corrente (par.6.4) - filo curvilineo

Filo curvilineo nel piano, campo uniforme PQ 0 S P 8 C Il Pall= e 5 B Q ds P F = iPQ x B

Figura 6.18 Forza su un filo conduttore di forma qualunque percorso da corrente in un campo magnetico uniforme.

a È non dipende dalle forme del conduttore se È è unforma ma solo del vettore PO a fanchè d'corrente la forse è identica si due conduttori P F = P (id5 1 B = id51B P = i PQ1 B Vale anche se il conduttore non i nul piano (es. molla)