Lezione 21: Statica dei fluidi, legge di Stevino e principio di Pascal

Lezione 21

• Moto circolare uniforme come moto armonico
• Moto armonico smorzato
• Oscillazioni forzate e risonanza

Statica dei fluidi

• Definizioni fluido e pressione

Cap. 14 Gettys

Lezione 20

Cap. 15 Gettys

• Legge di Stevino (incomprimibili / comprimibili)
• Misura della pressione: manometro e barometro
• Principio di Archimede

Fluidodinamica

• Tubo di flusso, portata di massa ed equazione di continuità
• Teorema di Bernoulli
• Applicazioni teorema Bernoulli (Venturi, Torricelli)

Cap. 15 Gettys

STUDIORU UNIVERSI UM . ALMA · A · PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica

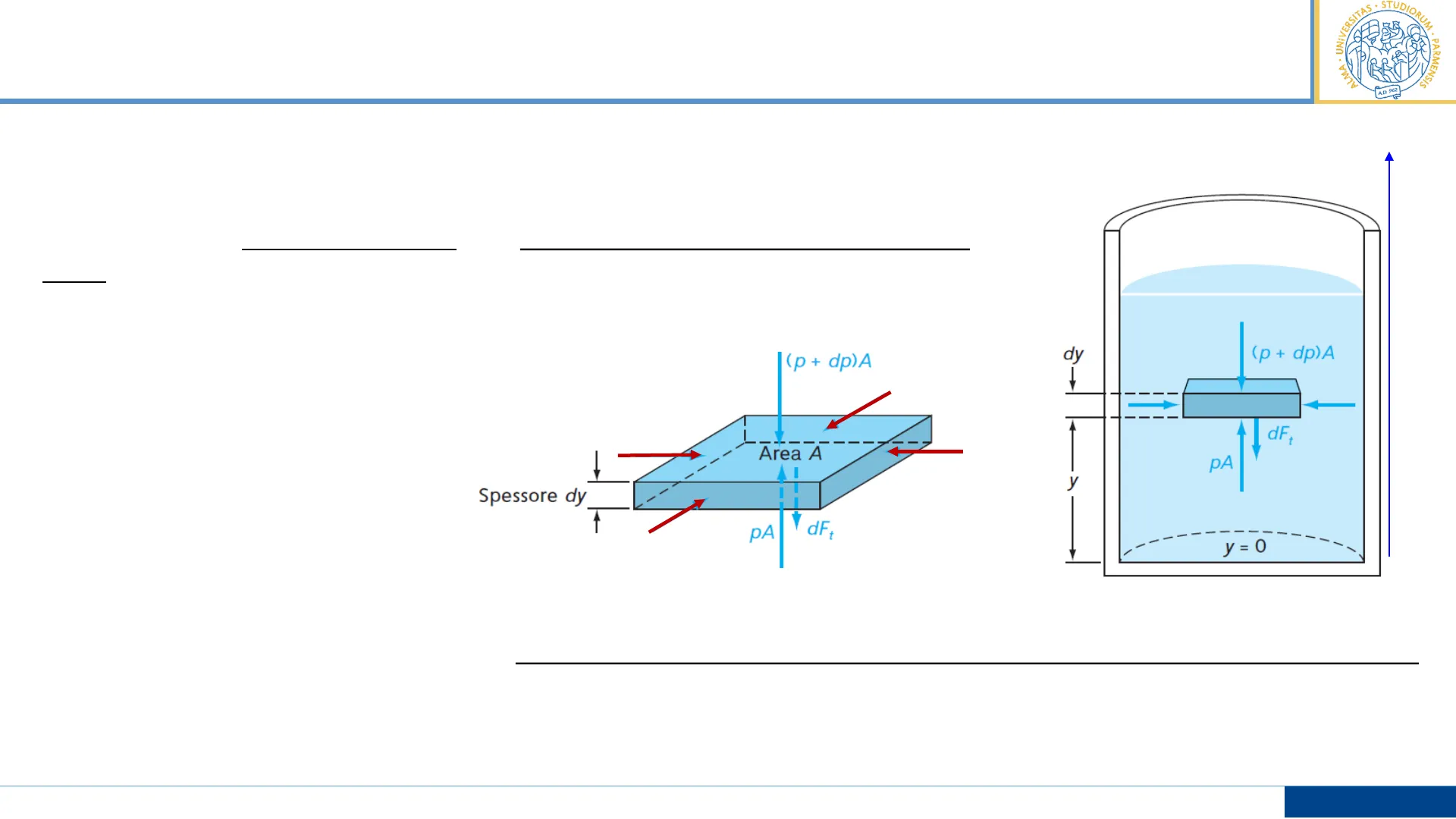
Statica del fluido

JERSI UM . ALMA · A . PARMENSIS A.D. 962 Consideriamo un fluido in quiete -- > esso esercita una forza normale alla superfice del contenitore o di qualsiasi oggetto in esso immerso Valutiamo effetto forza gravitazionale sulla variazione verticale della pressione in un fluido in equilibrio, ovvero valutiamo la pressione del fluido in funzione della profondità y Consideriamo elemento infinitesimo del fluido (area A e altezza dy) di peso dFt (p + dp)A Area A Spessore dy PA dFt y dy (p + dp)A dFt pA y y = 0 Dato che il fluido è in quiete (equilibrio) le forze laterali che agiscono su questo volumetto devono compensarsi esattamente Verticali non possono essere uguali -- > Forza inferiore (ovvero p inferiore, dato che A è la stessa) deve compensare dFt del volumetto stesso, altrimenti questo non si potrebbe trovare in quiete (ovvero "cadrebbe" verso il basso) P. Mazzolini Fisica I - LT Chimica 2

Pressione in funzione della profondità

STUDIORU VERSI UM . UN ALMA . A · PARMENSIS A.D. 962 p = pressione a livello y (p + dp) = pressione a livello (y + dy) p = F / A Area A dy dFt pA Essendo il fluido in equilibrio, le forze agenti sulla faccia superiore ed inferiore devono essere diverse: PA - (p + dp)A - dFt = 0 dFt = (dm)g = (pdV)g = pg(Ady) dpA + pg(Ady) = 0 dp = - pg dy La differenza di pressione dp compensa il peso dell'elemento di fluido Segno negativo -> la pressione diminuisce all'aumentare della quota dal fondo del recipiente (o aumenta andando dalla superficie verso il fondo del recipiente) P. Mazzolini Fisica I - LT Chimica 3 (p + dp)A y

Legge di Stevino

Integriamo l'equazione per ottenere la pressione in funzione dell'altezza y P2 P1 J, dp =~ [" y2 pg dy Considerando liquidi come incomprimibili -- > p costante (p2-P1) =- pg(y2-y1) Se superfice libera è in y2 (es. pelo dell'acqua) e la pressione su tale livello è po (pressione atmosferica) -- > a profondità h = y2 - 11 : Assoluta p = Po +pgh Relativa Po Po + pgh PRESSIONE IDROSTATICA Legge di Stevino p di un fluido incomprimibile aumenta linearmente con la profondità (ed è uguale in tutti i punti alla stessa profondità). Questo è indipendente dalla forma del contenitore utilizzato STUDIORU JERSI UM . UNI ALMA · A . PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica 4

Esempio di pressione sul fondo dell'oceano

Qual'è la pressione sul fondo dell'oceano in un punto in cui la sua profondità è h = 3 km? STUDIORU UNIVERSI DOD UM- ALMA · A · PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica 5

Principio di Pascal

STUDIORU JERSI UM- UNI ALMA A · PARMENSIS A.D. 962 La pressione applicata su un fluido confinato è trasmessa inalterata a tutti i punti nel fluido e alle pareti del contenitore -- > se po gravante sulla superficie aumenta di Ap, anche p alla profondità h aumenterà dello stesso Ap (Principio di Pascal) Ph = (Po + Ap) + pgh Sollevatore idraulico -- > contenitore chiuso con liquido incomprimibile all'interno e due pistoni di diversa area ai due estremi posti alla stessa quota. Applichiamo al pistone ad area minore a una forza f -- > questa si trasmetterà inalterata nel fluido, quindi in condizioni di equilibrio (statica), al pistone di area maggiore dovremo applicare una forza F maggiore Stessa quota = stessa p superfici su cui p è applicata # Con il sollevatore idraulico una data forza f può essere applicata per un certo spostamento del pistone ad area minore a, "trasformandola" in una forza maggiore F in un cilindro ad area maggiore A (spostamento però minore perchè volume di fluido spostato è il medesimo - fluido incomprimibile) Es. A = 100 a -> = --- > F = 100 f Ma allo stesso tempo se voglio alzare cilindro grande di 1 m, dovrò abbassare cilindro piccolo di 100 m (il lavoro compiuto dai due cilindri è il medesimo) F 4 A > a f = pa F = pA 1 pa PA P. Mazzolini Fisica I - LT Chimica 6

Fluidi comprimibili (gas)

STUDIORU UNIVERSI UM . A · PARMENSIS ALMA · A.D. 962 Se il fluido è comprimibile (solitamente gas) la sua densità varia in funzione dell'altezza Per molti gas (es. aria), data una temperatura costante ed i valori di pressione e densità ad una quota di riferimento (y = 0 -> Po, Po) vale: p/Po = P/ Po -- > P = Po P/Po Equazione della pressione in f(y) dp = - pg dy = - (Pop/Po)g dy d dp Pog Po dy Possiamo integrare questa equazione tra il livello di riferimento (y = 0) ed un livello h Jo h Pog Po dy In(p/po) In ph - In po = Pog Po (h -0) Ph In Po Pogh Po p(h) = poe-(Pogh/po) La pressione di un fluido comprimibile decresce con l'altezza P. Mazzolini Fisica I - LT Chimica 7

Esempi di pressione nei fluidi comprimibili

STUDIORU UNIVERSI BOD UM · ALMA . A · PARMENSIS A.D. 962 Es. Calcolare la differenza di pressione in una stanza alta 4 metri sapendo che la densità dell'aria a temperatura ambiente e a pressione atmosferica (po = 1.01 × 105 Pa ) vale Po = 1.29 kg/m3 Es. A quale altezza si ha una pressione che è la metà di quella al livello del mare (ipotesi che la temperatura sia la medesima)? monte bianco = 4800 m P. Mazzolini Fisica I - LT Chimica 8

Misurazione della pressione di un gas: manometro a tubo aperto

STUDIORU VERS UM . UNI ALMA . A · PARMENSIS A.D. 962 Serve a misurare la sovrapressione (o pressione relativa) di un gas dentro un recipiente chiuso Tubo ad U pieno di liquido (es. mercurio, Hg) Po = Patm (tubo aperto) PB = Patm + pgh (p densità del liquido) All'equilibrio, essendo C alla stessa altezza di B (livello 2), avremo anche la stessa pressione in questi due punti -- > essendo C collegato al volume chiuso contente il gas di pressione incognita p: p = PB = Po + pgh Po A Livello 1 h P Livello 2 C B Serbatoio Manometro La pressione p è chiamata pressione assoluta, mentre pr = p - Patm = pgh è chiamata pressione relativa P. Mazzolini Fisica I - LT Chimica 9

Misurazione della pressione atmosferica: barometro

STUDIORU VERSI UM . ALMA . A . PARMENSIS A.D. 962 Tubo chiuso ad un estremo lungo almeno 800 mm riempito fino all'orlo di Hg (PHg ~ 13.6 x 103 kg/m3 -- circa 13 volte la densità dell'acqua) -- > tappo estremità Si capovolge il tubo in una vasca contenente anch'essa Hg e si toglie il tappo Il livello di Hg nel tubo immerso calerà fino a determinata altezza h rispetto al livello di Hg nella bacinella. Essendo stato il tubo pieno e tappato fino all'immersione nella bacinella di Hg, nel tratto svuotato del tubo possiamo considerare la sua pressione nulla Patm - Ph = pgh La pressione atmosferica è uguale alla pressione causata dalla colonna di mercurio -- > 1 atm = 760 mm di Hg (ovvero 1 Torr) p-> 0 Patm 1 Prima Dopo Barometro ad acqua è fattibile allo stesso modo, ma data la densità circa 13 volte minore al Hg, per vedere la "rottura" della colonna d'acqua e poter misurare la pressione atmosferica dovrei avere una colonna di altezza pari a circa 10 m P. Mazzolini Fisica I - LT Chimica 10

Principio di Archimede

UNIVERSI STUDIORU UM- ALMA · A.D. 962 Oggetto cilindrico che si trova in liquido (densità p) in equilibrio > essendo in galleggiamento, la forza sulla sezione orizzontale superiore sarà dovuta alla pressione atmosferica po (barometrica), mentre quella sulla sezione inferiore alla pressione idrostatica (funzione della profondità nel fluido) p = Po + pgh Fsup = PoA Finf = (p +pgh)A Per essere in equilibrio Finf - Fsup - Mg = 0 Vimmerso La risultante di queste due forze è la forza di Archimede FA = Finf - Fsup = pghA FA = (Vimmersop)g = mliquido g Un corpo immerso parzialmente o totalmente in un fluido riceve una spinta di intensità pari al peso del fluido spostato diretta verso l'alto lungo la retta passante per il centro di massa del fluido spostato Fsup A Pcil L C ℎ ¥Mg A S Finf fluido (densità p) Per avere galleggiamento FA = Mg -> pghA = ALPcilg h < L > Poggetto < Pfluido P. Mazzolini Fisica I - LT Chimica 11 A · PARMENSIS

Stabilità di galleggiamento

STUDIORU ERS UM . ALMA A · PARMENSIS A.D. 962 Un corpo immerso parzialmente o totalmente in un fluido riceve una spinta di intensità pari al peso del fluido spostato diretta verso l'alto lungo la retta passante per il centro di massa del fluido spostato Oggetto che galleggia in acqua > il suo centro di massa di norma non coincide con il centro di massa del volume di liquido spostato (punto in cui si applica la forza di Archimede). Se forza peso del corpo e forza di Archimede non si trovano sulla stessa retta di azione ho un momento torcente > Tz di richiamo verso posizione di equilibrio Tz = 0 solo quando Fg ed FA giaceranno sulla stessa retta d'azione ! Un centro di massa del corpo in galleggiamento basso porta alta stabilità del corpo in galleggiamento (progettazione barche) > se il centro di massa si sposta verso la superficie si rischia capovolgimento del corpo! S P. Mazzolini Fisica I - LT Chimica 12 FA Mg S

Esempio di asta sottile in acqua

Asta sottile di lunghezza I, sezione S e densità p è parzialmente immersa in un contenitore d'acqua. Una sua estremità è incernierata alla parete di un contenitore O. All'equilibrio parte di lunghezza d si trova fuori dall'acqua (Po)- Determinare la densità del materiale di cui è composta l'asta. STUDIORU VERSI UM. UNI ALMA . A . PARMENSIS A.D. 962 O d θ L P. Mazzolini Fisica I - LT Chimica 13

Fluidi ideali in movimento

STUDIORU UNIVERSI UM . ALMA . A . PARMENSIS A.D. 962 Argomento di difficile trattazione > non seguimo moto di una singola particella di fluido, ma focalizziamo attenzione su un punto dal quale fluiscono le particelle del fluido e ne determiniamo le proprietà fisiche (p, p,¿) Consideriamo il moto di un fluido in condizioni stazionarie, ovvero un fluido in moto laminare (non turbolento) > tutti gli elementi di fluido che passano in determinato punto hanno le stesse p, p, ¿ A B VB VA C VC Linee di flusso > linee lungo le quali fluiscono le particelle (evidenziabili da un tracciante colorato come in figura). In ogni punto la tangente alla traiettoria coincide con la direzione della ¿ del fluido. Linee di flusso in un fluido stazionario NON variano nel tempo (particella di fluido che percorre una determinata linea di flusso avrà sempre stesse proprietà fisiche) P. Mazzolini Fisica I - LT Chimica 14