Lezione 8: Lavoro compiuto da forze variabili e teorema lavoro-energia

Lezione 8

• Forze di attrito dinamico e viscoso

Cap. 6 Gettys

Lezione 7

• Lavoro compiuto da forza costante
• Lavoro compiuto da forza variabile 1d (esempio molla)

Cap. 8 Gettys

• Lavoro compiuto da forza variabile in 3d
• Teorema lavoro-energia cinetica
• Potenza
• Sistemi conservativi e forze conservative
• Energia potenziale e conservazione energia meccanica

Cap. 8 Gettys Cap. 9 Gettys STUDIORU UNIVERSI UM . A · PARMENSIS ALMA · A.D. 962 P. Mazzolini Fisica I - LT Chimica

Lavoro compiuto da una forza variabile in spazio 3d

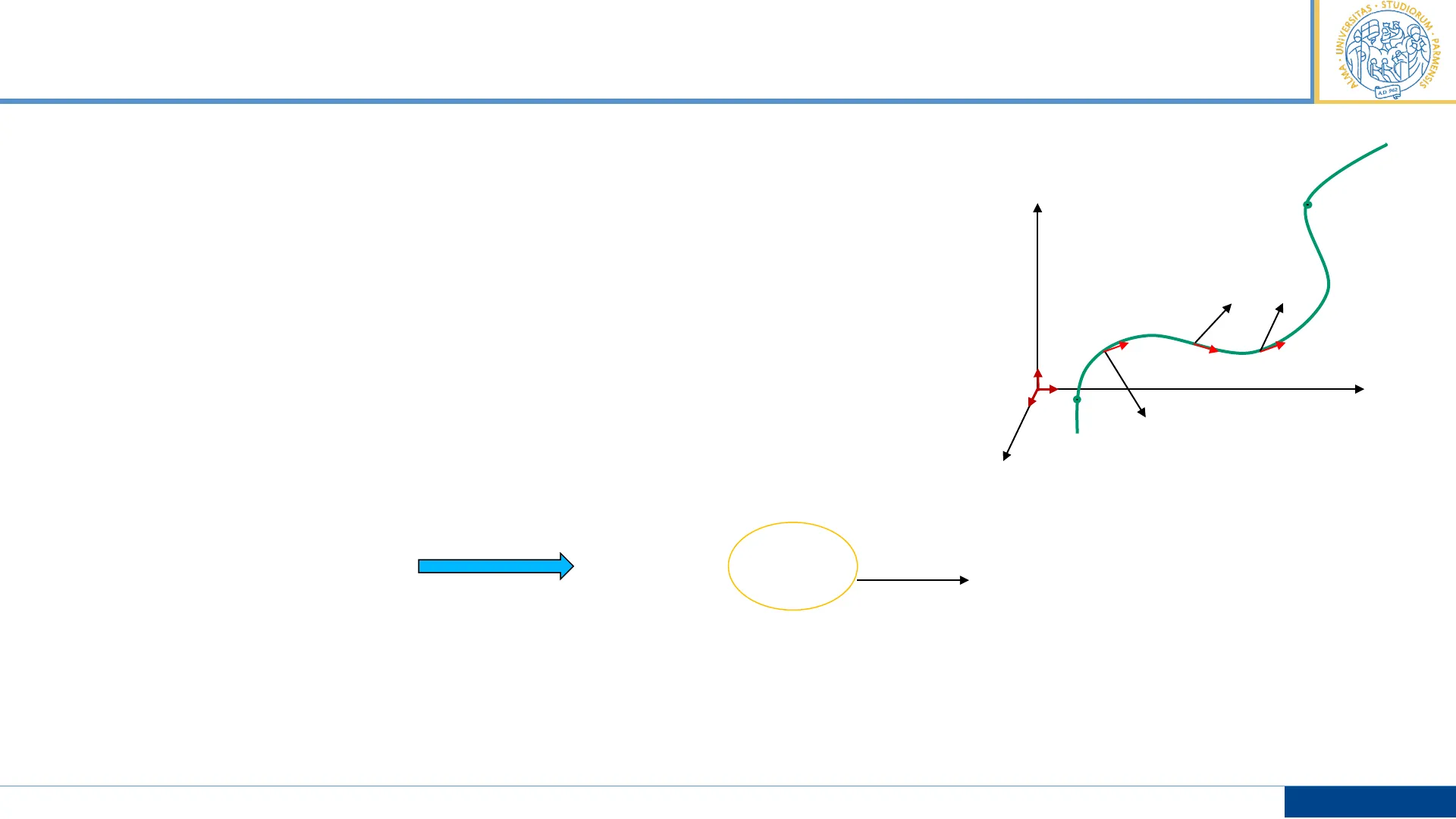
VERSI UM . UN ALMA . A . PARMENSIS A.D. 962 Traiettoria generica tridimensionale di un corpo sottoposto ad una forza F variabile. Dividiamo in piccoli segmenti la curva > piccoli spostamenti Ar Considerando costante la forza applicata F al corpo lungo questo piccolo spostamento Ar, posso esprimere il lavoro di quel tratto come: Aw = F . Ar E come visto prima, potremmo approssimare il lavoro compiuto dalla forza variabile F (r) sommando il contributo degli n trattini in cui abbiamo suddiviso la traiettoria

y f F F Ář AT î k X F Z passaggio al limite Wa n SF - AP W & W = i F . dr i=1 Possiamo esprimerlo in funzione delle sue componenti lungo assi cartesiani F·dř= (Fxî +F}} +F2k) · (dxî +dyĵ+dzk) P. Mazzolini Fisica I - LT Chimica

Lavoro compiuto da una forza variabile in spazio 3d

STUDIORU VERSI UM . UN ALMA . A . PARMENSIS A.D. 962 w = W = i F . dr F · dr = (Fxî + FyÎ + Fzk) · (dxî + dyĵ + dzk) componenti ortogonali saranno nulle nel caso del prodotto scalare > rimangono solo le componenti equidirette ↑ · = ↑ · k=j · R = 0 (più loro permutazione per proprietà commutativa) F . dr = Fxdx + Fydy + Fzdz

y f F F AT AT î k X F Z W = i (Fxdx + Fydy + Fzdz) P. Mazzolini Fisica I - LT Chimica

Lavoro compiuto dalla forza gravitazionale in 3d

STUDIORU UNIVERSI UM . ALMA · A.D. 962 Consideriamo una traiettoria arbitraria di un corpo in x,y,z. Sul corpo possono agire diverse forze, ma noi possiamo sempre valutare i singoli lavori effettuati da ognuna di esse > ci concentriamo sulla valutazione del lavoro compiuto da Fg sul corpo nella traiettoria tra il punto iniziale i e finale f La forza gravitazionale è puramente verticale -> Fg = Fg,y = (-mg)} Pg · dî = (Fg,ydy)}·Î=Fgydy

Fg · dr W = 1. yi yi Fg,ydy = |(-mg)dy = - mg dy 'yi

y f i î k X Z W = i y f Lavoro compiuto da Fg sul corpo è indipendente dalla sua traiettoria, ma solo dalle quote iniziali e finali del corpo stesso W = - mg (yf - yi) P. Mazzolini Fisica I - LT Chimica

Teorema lavoro-energia (1d)

STUDIORU UNIVERSI UM . ALMA · A.D. 962 Consideriamo caso monodimensionale di corpo di massa m sottoposto alla forza F costante puramente orizzontale > F = Fxî Assumendo di non avere attrito tra corpo e pavimento: 2º principio dinamica -> Fx = måx = maxÎ

xi 10 Xf x Il lavoro compiuto dalla forza F sul corpo nello spostamento d vale w = Fx · d = Fxdî · î = Fxd = max(Xf-Xi)

. 02 W = max 1 Fax(+2 -t2)= 1 2 = - m(azt} 2+ azt?) 1 W = = mvf - mv; 2 2 1 W compiuto da una F costante è proporzionale alla differenza dei quadrati delle velocità -> quando una F compie lavoro su un corpo, allora ne cambia la velocità P. Mazzolini Fisica I - LT Chimica

◌⃗ Dal momento che il corpo si muove di moto uniformemente accelerato lungo x 1 d = = axt2 Vx = axt

Energia cinetica

w = = mv? - - mv? 1 1 Teorema lavoro-energia · w > 0 > Lavoro fatto su un corpo e positivo, allora il corpo aumenterà il modulo della sua velocità ( vf > |vil) · w < 0 > Lavoro fatto su un corpo è negativo, allora il corpo diminuirà il modulo della sua velocità ( vf < \ vil) · w = 0 > Lavoro fatto su un corpo è nullo, allora il corpo avrà mantenuto il modulo della sua velocità ( vf = 10il) Quantità =mv2 definita come energia cinetica K di un corpo 1 K = = mv2 2 · Energia e lavoro sono entrambe misurate in [J] · Un oggetto fermo non ha energia cinetica · Un oggetto in movimento ha sempre energia cinetica positiva (v2) STUDIORU UNIVERSI UM . A · PARMENSIS ALMA · A.D. 962 W può essere negativo, ma K no P. Mazzolini Fisica I - LT Chimica

Teorema lavoro-energia generalizzato (3d con forze variabili)

STUDIORU VERSI UM . UNI ALMA · A · PARMENSIS A.D. 962 Generalizziamo il teorema lavoro-energia per diverse forze agenti su un corpo che si muove su una traiettoria 3d Per il 2º principio, sappiamo che la risultante delle forze agenti sul corpo sarà Possiamo allora descrivere il lavoro della forza risultante F = må v-‘(IF).dr=mjä·dř Sviluppiamo il prodotto scalare: å · dr = (axî + ay] + azk) · (dxî + dyĵ + dzk) Per prop. prodotto scalare å · dr = axdx + aydy + azdz Sapendo che le componenti della velocità e dell'accelerazione possono essere espresse come dt dx Vx = dvx ax = dt a · dr = dvx dť 4 At ) + de dt (vydt) + dt dvz dvy (vzdt) w = m 'vi (Vxdvx + Vydvy + vzdvz) Integrale di una somma = somma degli integrali w = = m (v2 + v2 + v2) 1 Vi P. Mazzolini Fisica I - LT Chimica

Teorema lavoro-energia generalizzato (3d con forze variabili)

STUDIORU UNIVERSI UM . A · PARMENSIS ALMA · A.D. 962 w == m(v2+ v} + v2) 1 Vi jVf Modulo quadrato del vettore 1 > v2 = 12 + v3 + v2 1 == m (v2)\" =mv ?- mvį 1 Il lavoro totale della risultante delle forze agenti su un corpo che si muove in uno spazio tridimensionale è pari alla variazione della sua energia cinetica tra fine e inizio traiettoria P. Mazzolini Fisica I - LT Chimica

Esempio

Una persona spinge un bicchiere di massa m = 0.2 kg lungo un tavolo piano con una forza di modulo F = 2 N ad un angolo 0 = 30° rispetto all'orizzontale per una distanza di d = 0.5 m. Il coefficiente di attrito tra il tavolo ed il bicchiere è pari a uk = 0.1. Se il bicchiere si trovava inizialmente fermo sul tavolo, quale sarà l'energia cinetica e la velocità finale del bicchiere?

◌⃗ Il lavoro totale svolto sul bicchiere è dato dalla risultante delle forze agenti su di esso. Questo può essere suddiviso nelle due componenti x,y. Sull'asse y, la risultante delle forze è pari a 0 in quanto il bicchiere non varia il suo moto lungo quest'asse

FN 0 = 30° ◌⃗ ◌⃗ k Fg STUDIORU ERS UM . UN ALMA . A · PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica

Potenza

STUDIORU JERSI UM ALMA . A . PARMENSIS A.D. 962 La potenza esprime la rapidità con cui viene sviluppata una certa quantità di lavoro. Se un lavoro W è svolto da una forza nell'intervallo di tempo At, allora la potenza media si definisce come: (P) = W At W La potenza istantanea P esprime la rapidità istantanea con la quale viene svolto un lavoro (ovvero considerando intervalli di tempo At -> 0) : P = dW dt Dimensioni di [ML2T-3] Nel SI si misura in [ ] /s ] = [ W] Watt Un modo alternativo per definirla può essere ottenuto esplicitando il lavoro dW P = dt Spesso la potenza viene utilizzata come variazione di energia > AE = P At da cui deriva un'altra unità di misura dell'energia che usiamo spesso [kWh] P. Mazzolini Fisica I - LT Chimica

Esempio

STUDIORU ERS UM . UN ALMA . A · PARMENSIS A.D. 962 Palla di massa m = 0.2 kg che viene lasciata da ferma da un'altezza yo = 15 m e cade fino a raggiungere un'altezza pari a yf = 5 m. Determinare la potenza media esercitata dalla forza di gravità sulla palla (ignorare attrito dell'aria) e quale sia la potenza istantanea quando la palla si trova a yf = 5 m

yo yf P. Mazzolini Fisica I - LT Chimica

Esempio

STUDIORU IERS UM . UN ALMA A . PARMENSIS A.D. 962 Auto di massa m = 1000 kg sviluppa una potenza media di 50 cavalli vapore (1 cv = 735 W) accelerando da ferma. Calcolare il tempo minimo perchè raggiunga una vf = 100km = 27.8 m ........ P. Mazzolini Fisica I - LT Chimica

Sistema conservativo

STUDIORU VERSI UM . UN ALMA · A · PARMENSIS A.D. 962 Un sistema conservativo è un sistema nel quale l'energia si conserva, ovvero sistemi nei quali sul corpo considerato agiscono solo forze conservative W = Σ 1 · dr i Quando il lavoro compiuto dalle forze E agenti sul corpo per andare da un punto iniziale i ad un punto finale f è indipendente dalla traiettoria del corpo (dal percorso) -- > solo forze conservative stanno agendo sul corpo Quando il lavoro compiuto dalle forze F agenti sul corpo per andare da un punto iniziale i ad un punto finale f è dipendente dalla traiettoria del corpo (dal percorso) -- > sul corpo agiscono anche delle forze dissipative (non conservative) P. Mazzolini Fisica I - LT Chimica

Forza conservativa come integrale di circuitazione nullo

STUDIORU UNIVERSI UM . ALMA · A · PARMENSIS A.D. 962 Conseguenza del fatto che il lavoro svolto da una forza conservativa dipende solo dal punto i e f della traiettoria -- > considerando i = f, ovvero una traiettoria chiusa qualsiasi, il lavoro di una forza conservativa è nullo

y [m] i= f w = 0 F . dř = 0 x [m] z [m] P. Mazzolini Fisica I - LT Chimica

Forza gravitazionale come forze conservativa

VERSI UM . UNI ALMA · A · PARMENSIS A.D. 962 La forza di gravità Fg è un esempio di forza conservativa (visto in Lezione 7) La forza gravitazionale è puramente verticale > Èg = Fg,y] = (-mg)}

y f i Ĵ î X Z 1 W = Fg,ydy = Jyi [" (-mg)dy = - mg [" dy Jyi Lavoro compiuto da Fg sul corpo è indipendente dalla sua traiettoria, ma solo dalle quote iniziali e finali del corpo stesso W = - mg (yf - yi) P. Mazzolini Fisica I - LT Chimica

w : S. i yf yi Èg · dî = (Fg,ydy)}·Î=Fg,ydy STUDIORU

Esempio: circuitazione forza gravitazionale

Abbiamo definito la forza di gravità come una forza conservativa. Di conseguenza deve valere: w = 0 Fg·dř=0 Creo un circuito chiuso, ovvero una traiettoria del corpo che preveda che la posizione finale sia uguale alla posizione di partenza (1).

2 3 1 4 mg Studiamo il lavoro effettuato dalla sola forza T1-2 -- > lavoro sarà negativo (Fg e 71-2 opposti in direzione, 0=180°) -- > W1-2 = - mg(y2 - y1) = - mgAy T2-3 -- > lavoro sarà nullo (Fg e 72-3 sono ortogonali, 0=90°) -- > W2-3 = 0 T3-4 -- > lavoro sarà positivo (Fg e 73-4 allineati, 0=0°) -- > W3-4 = - mg(y4 - y3) = mgAy T4-1 -- > lavoro sarà nullo (Fg e 14-1 sono ortogonali, 0=90°) -- > W4-1 = 0 w = 0 Fg · dr = 0 STUDIORU VERS UM . ALMA . A · PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica