Lezione di fisica: equilibrio statico del corpo rigido e moto rotatorio

Lezione 12

• Urti e loro classificazione
• Urti elastici in una dimensione

. Cenno ad urti elastici in 2d . Urti totalmente anelastici . Pendolo balistico Cap. 10 Gettys

Lezione 11

Equilibrio statico del corpo rigido

• Momento di una forza

. Condizioni di equilibrio statico

• Baricentro

Cinematica del moto rotatorio

• Coordinata

Cap. 11 Gettys Cap. 12 Gettys

STUDIORU UNIVERSI UM . ALMA · A · PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica

Da punto materiale a corpo rigido

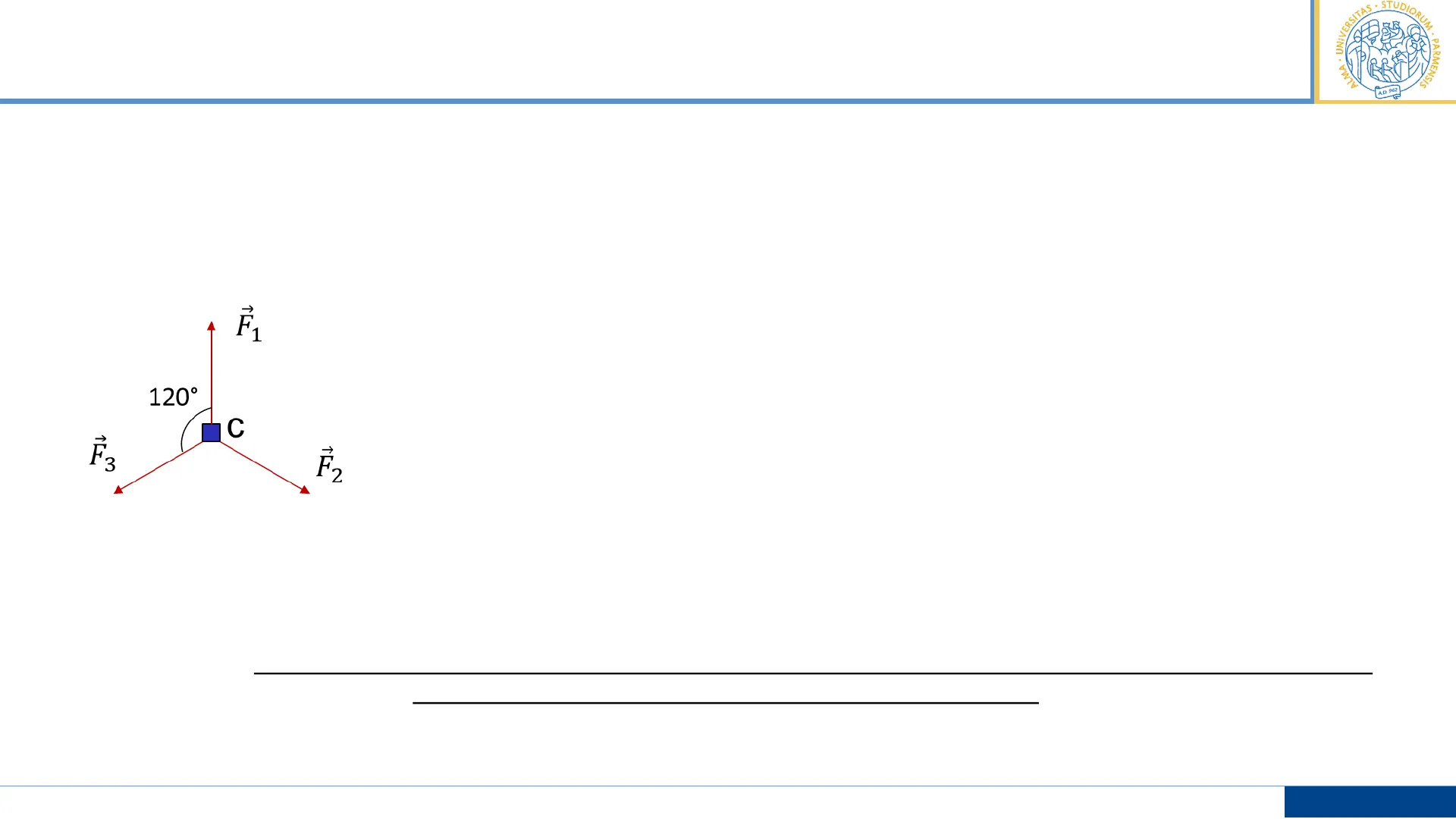
STUDIORU JERSI UM . A . PARMENSIS ALMA A.D. 962 Considerando un punto materiale, abbiamo visto (L 5) che la condizione necessaria per rimanere in uno stato di quiete (o moto rettilineo uniforme) è che la sommatoria delle forze su esso applicato sia nulla SF = 11 + F2 + P3 = 0 - 120° C Nel caso di un corpo esteso, questo sarà in equilibrio statico se OGNI suo punto è in quiete e rimane in quiete Per la nostra trattazione semplificata considereremo esclusivamente corpi rigidi (indeformabili, o meglio con deformazioni trascurabili) -- > corpi nei quali la distanza relativa fra i punti che lo compongono rimane costante nel tempo anche in conseguenza all'applicazione su di essi di una o più forze P. Mazzolini Fisica I - LT Chimica

Corpo rigido, moto traslatorio ed equilibrio traslatorio

In L9 abbiamo visto che il centro di massa è un punto "speciale" di un generico corpo esteso (o di un sistema di corpi interagenti) in cui possiamo considerare che tutta la massa M del corpo/sistema sia condensata -> il moto del cm è determinato dalle sole forze esterne Måcm = Σ ◌⃗ est Con sommatoria forze esterne nulla il cm non possiede un'accelerazione, ovvero esso mantiene il suo stato di quiete o di moto rettilineo uniforme (ovvero la sua quantità di moto si conserva -- > L10, anche se in questo esempio non si trattava di corpo rigido, il concetto del CM è il medesimo e sempre valido!) · STUDIORU IVERSI DOD UM . UNIV ALMA · A · PARMENSIS A.D. 962 Centro di massa Do non è corpo rigido ( CM ) P. Mazzolini Fisica I - LT Chimica

Moto traslatorio ed equilibrio traslatorio di un corpo rigido

JERSI UM . UN ALMA · A · PARMENSIS A.D. 962 Un corpo rigido è in moto puramente traslatorio quando in un certo intervallo di tempo At tutti i suoi punti si spostano dello stesso vettore Ar, ovvero se il vettore velocità vi di ognuno dei punti che lo compongono è il medesimo vi vi vi ◌⃗ Consideriamo ora il centro di massa di questo corpo rigido > possiamo definire che il corpo si trova in equilibrio traslatorio quando il suo centro di massa ha accelerazione nulla (il cm rimane in quiete o in moto rettilineo uniforme) Måcm = Fest = 0 ◌⃗ est,1 -- Fest,2 P. Mazzolini Fisica I - LT Chimica

Condizione di equilibrio traslatorio

! La condizione di equilibrio traslatorio del centro di massa è condizione necessaria, ma non sufficiente per avere equilibrio statico di un corpo esteso! Es. rotazione attorno al suo centro di massa

Cenni alla rotazione di un corpo rigido

STUDIORU JERSI UM . UNI ALMA · A . PARMENSIS A.D. 962 ΔΘ Porta fissata su un lato dai cardini Moto rotatorio: ogni punto del corpo rigido spazza lo stesso angolo 40 nello stesso intervallo di tempo At Per descrivere il moto rotatorio dovuto all'effetto di una o più forze applicate su un corpo rigido è fondamentale conoscere: • l'asse di rotazione del corpo · il punto di applicazione delle forze rispetto all'asse di rotazione · l'angolo tra la retta di azione del vettore forza ed il vettore distanza dall'asse di rotazione (vettore distanza tra asse di rotazione e punto di applicazione della forza applicata) P. Mazzolini Fisica I - LT Chimica

Introduzione al momento torcente

ERS POD ALMA A · PARMENSIS A.D. 962 Consideriamo un generico corpo esteso (rigido), libero di ruotare attorno ad un asse passante per il punto O (ortogonale al piano della sezione del corpo riportata in figura). Una forza F viene applicata al punto P del corpo. Rispetto all'asse di rotazione O, possiamo identificare il vettore r che identifica il punto di applicazione P della forza Per capire come F provochi una rotazione del corpo rispetto all'asse O scomponiamola in due componenti: • Fr diretta lungo la direzione del vettore r', la cui componente scalare vale Fr = F cos 0 • F diretta ortogonalmente alla direzione del vettore r F = F sin 0 ◌⃗ TRI 𝜃𝜃 ◌⃗ ◌⃗ P O 0 ◌⃗ ⊥ è solo la componente F1 che contribuisce alla rotazione del corpo rispetto all'asse O ed il suo effetto è tanto maggiore quanto maggiore è la distanza dall'asse di rotazione alla quale questa è stata applicata! Intensità (modulo) del momento torcente di una forza rispetto all'asse di rotazione O T = rF1 =r F = rFsin 0 Alternativamente può essere definita la componente r1 = r sin 0 (braccio di F) P. Mazzolini Fisica I - LT Chimica

Vettore momento torcente

STUDIORU IERS 91 UNI ALMA . A · PARMENSIS A.D. 962 Sappiamo valutare l'intensità (modulo) di un momento torcente applicato ad un corpo rigido esteso, ma questo NON basta! Il momento torcente è un vettore dato dal prodotto vettoriale: ₹=rxF ¿= řxF Ha le dimensioni [L2MT-2] e si misura nel SI in [Nm] ◌⃗ ◌⃗ ⊥ O 1 θ -- ◌⃗ ⊥ Da L2 sappiamo che: • il suo modulo vale t = rF_ = 11F = rF sin 0 (graficamente area verde a sn) . il prodotto vettoriale NON è commutativo (rx F + F X 7) . la direzione del vettore t è ortogonale al piano contenente i vettori r ed F . Il verso del vettore t è dato dalla regola della mano destra (uscente positivo, ovvero rotazione del corpo in senso antiorario causata da ť positivo) ◌⃗ ◌⃗ ⊥ ◌⃗ Fr P O 15 1 P. Mazzolini Fisica I - LT Chimica

Vettore momento torcente in corpo rigido

UM .STUDIORU ERS 91 UM . ALMA . A . PARMENSIS A.D. 962 Data una forza esterna di modulo costante e fissato il punto di applicazione della forza rispetto all'asse di rotazione del corpo considerato (es. consideriamo una porta e la distanza di applicazione di F rispetto ai cardini), il momento torcente ? avrà modulo massimo quando la retta d'azione di F sarà esattamente ortogonale al vettore ? (F1, direzione di ₹1 lungo asse di rotazione O, verso positivo), mentre sarà nullo se la retta di azione della forza interseca l'asse di rotazione (ovvero se la forza sarà allineata al vettore r, es. F2). ◌⃗ 1 F2 ◌⃗ ◌⃗ 1 O Se più forze esterne agiscono sul corpo rigido, tutti i momenti ad esse associate calcolati rispetto all'asse di rotazione considerato (es. O) devono essere considerati: la loro somma prende il nome di momento torcente risultante (o netto) : i=1 n Tnet,0 = ři × Fi,est P. Mazzolini Fisica I - LT Chimica

Condizioni per l'equilibrio statico di un corpo rigido

STUDIORU JERSI UM . UNI ALMA · A . PARMENSIS A.D. 962 Affinché un corpo rigido si trovi in equilibrio statico, dovranno essere soddisfatti contemporaneamente: Equilibrio traslazionale Per essere in equilibrio traslazionale, deve essere nulla l'accelerazione del centro di massa, ovvero la risultante delle forze esterne agenti sul corpo rigido Måcm = 0 I Fest = 0 Equilibrio rotazionale Per essere in equilibrio rotatorio, la sommatoria di tutti i momenti delle forze esterne agenti sul corpo valutati rispetto ad un qualunque asse di rotazione O (scegliamo "il più conveniente") deve essere nulla > test =0 Ciascuna di queste equazioni vettoriali può avere componenti nei tre assi (x, y, z). Per semplicità, noi considereremo solo il caso di forze complanari, ovvero forze agenti sul piano (x,y) > questo garantisce di avere solo momenti torcenti orientati lungo la direzione dell'asse z. Le condizioni di equilibrio statico si riducono così a 3 equazioni: Σ Fest,x Σ Fest,y ΣTest,z P. Mazzolini Fisica I - LT Chimica

Centro di gravità o baricentro

STUDIORU UM . A . PARMENSIS ALMA A.D. 962 In esercizi di statica (ma non solo!) che hanno a che fare con un corpo rigido esteso, avremo sempre a che fare con la sua forza peso. Il punto di applicazione di tale forza è il baricentro. Dimostriamo che il baricentro ed il centro di massa, in un campo gravitazionale costante (non dipendente da y), sono coincidenti Y ? . o x mig Fp = Mg Consideriamo un corpo rigido come un insieme di punti estesi di massa discreta mį. Fissiamo gli assi di riferimento e consideriamo y parallela all'accelerazione gravitazionale g. Il peso di ciascuna massa discreta mi è puramente verticale e se posso considerare il modulo di g costante, sommando i pesi dei singoli elementi di massa del corpo ottengo il modulo del peso totale: Fp = Emig = gEmi =Mg Non sappiamo però ancora dove questa forza peso totale andrà applicata P. Mazzolini Fisica I - LT Chimica

Calcolo dei momenti torcenti e baricentro

Sappiamo che per il calcolo dei momenti torcenti rispetto al generico punto O scelto come asse di rotazione, dobbiamo anche valutare per ognuno degli elementi di massa mi la distanza x¡ rispetto all'origine degli assi scelta come centro di rotazione (la forza peso è l'unica forza esterna in gioco, puramente lungo y > per i momenti in questa orientazione del corpo valutiamo x). Y Xcg o Xi x mig Fp = Mg 16 est,o => Testzi,O gmixi Il baricentro è quel punto in cui si può immaginare che sia applicato il peso totale del corpo in modo da produrre lo stesso momento totale sul corpo Tz,0 = XcgFp = Xcg Σ mi g Quindi posso riscrivere la coordinata X del centro di gravità Xcg > mig = > gmiXi Xcg Emig E gmixi = Emixi Emi = Xcm Se l'accelerazione dovuta a g è la stessa per ciascuna parte del corpo, il centro di gravità coincide con il centro di massa (rivedere L9) STUDIORU ERS UM- ALMA A . PARMENSIS A.D. 962 P. Mazzolini Fisica I - LT Chimica

Determinazione sperimentale del baricentro

STUDIORU UNIVERSI UM . ALMA · A · PARMENSIS A.D. 962 - I I Baricentro Attaccare il corpo ad un appoggio (filo al soffitto) > quando corpo è fermo vuole dire che non ci sono momenti torcenti che lo facciano oscillare, ovvero la sua forza peso (applicata al baricentro) deve essere allineata lungo la retta d'azione passante per il filo (non c'è braccio tra la forza peso ed il baricentro). > vario posizione filo e trovo seconda retta passante per il baricentro > Intersezione delle due rette mi darà la posizione del baricentro P. Mazzolini Fisica I - LT Chimica