Livello Fisico e Sistema Binario in Informatica: Operazioni Logiche AND e OR

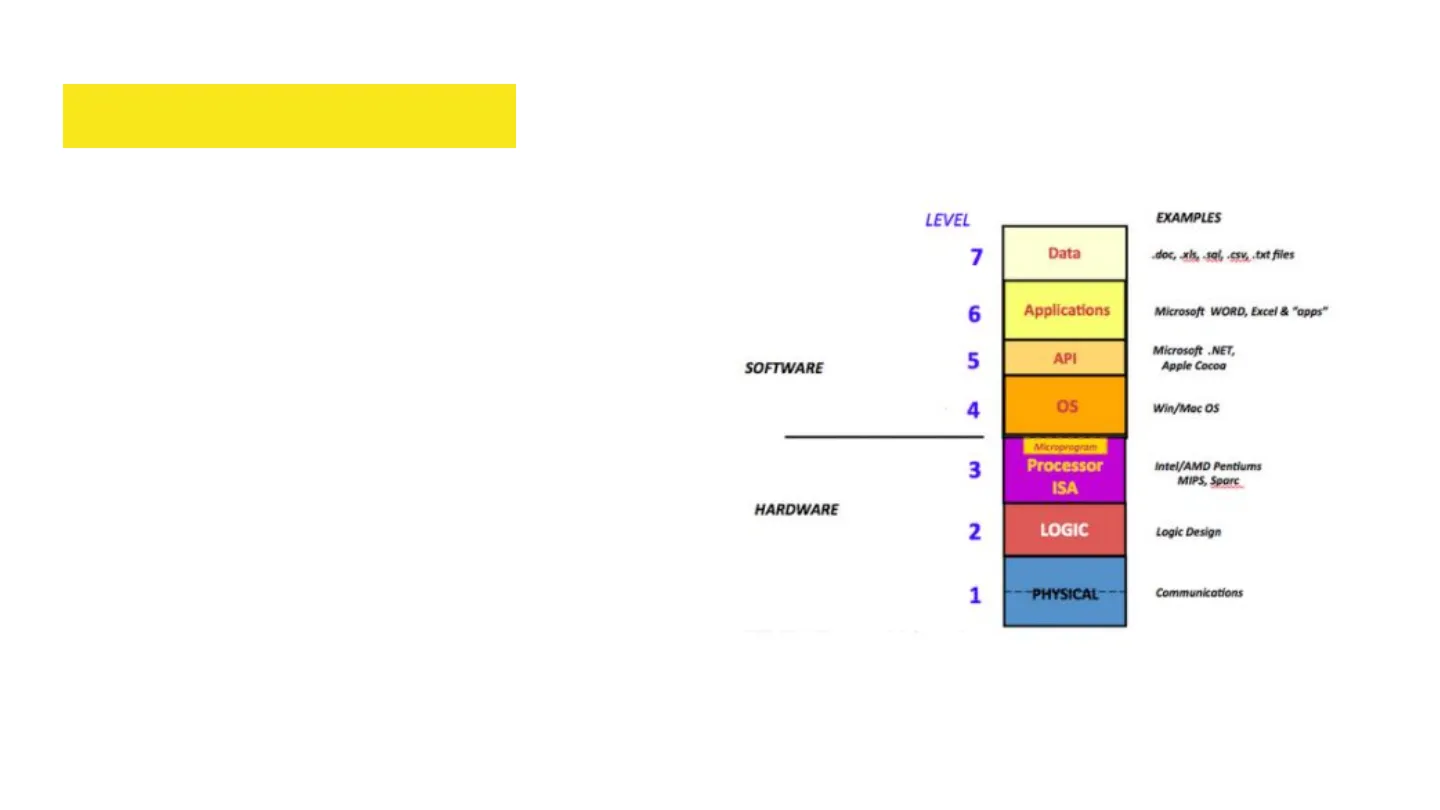
LIVELLO FISICO

Al livello più basso nel computer tutto è rappresentato da un segnale elettrico binario che può "esistere" solo in due stati fisici ben definiti: acceso (nel caso si registri un passaggio di corrente elettrica) o spento (se non si registra il passaggio di corrente elettrica). Questi stati fisici sono rappresentati nel linguaggio del computer attraverso un sistema binario che consente al processore di un qualunque sistema informatico di eseguire le operazioni alla base dei moderni software e applicativi.

LEVEL 7 Data Applications Microsoft WORD, Excel & "apps" Microsoft .NET, Apple Cocoa Win/Mac OS 3 HARDWARE 2 1 EXAMPLES .doc, als, sal, .csv, .txt files 6 5 API SOFTWARE Os 4 Microprogram Processor ISA Intel/AMD Pentiums MIPS, Sparc LOGIC Logic Design PHYSICAL Communications

SISTEMA BINARIO

Il sistema numerico binario è un sistema numerico posizionale in base 2. Esso utilizza solo due simboli, di solito indicati con 0 e 1, invece delle dieci cifre utilizzate dal sistema numerico decimale. Ciascuno dei numeri espressi nel sistema numerico binario è definito "numero binario".

11001100111001000000 110010101110010001 00000110000101110000 0010011000016 01110000 10110111001100111001 01110010011101 11011 001000000111000001100

SISTEMA BINARIO IN INFORMATICA

In informatica il sistema binario è utilizzato per la rappresentazione interna dell'informazione dalla quasi totalità degli elaboratori elettronici, in quanto le caratteristiche fisiche dei circuiti digitali rendono molto conveniente la gestione di due soli valori, rappresentati fisicamente da due diversi livelli di tensione elettrica. Tali valori assumono convenzionalmente il significato numerico di 0 e 1 o quelli di vero e falso della logica booleana.

B3 B2 B1 000 0 1 2 001 010 011 3 100 4 101 5 110 6 111 - 7

DA BINARIO A DECIMALE

La formula per convertire un numero da binario a decimale d_n si indica la cifra di posizione n all'interno del numero, contate da destra verso sinistra iniziando da 0) è: d 2" + d_ 2" + ... + d 21 + d + 2° = N1 n-1 Per esempio: 1001= 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0=9

5 4 3 1 0 2 2 2 2 2 2 2 peso: 32 16 8 4 2 1 V / V V V V 101101

DA DECIMALE A BINARIO

Invece per convertire un numero decimale a binario bisogna dividere il numero per 2 finchè diventa 0. Ad ogni passaggio, bisogna conservare i resti ed infine scriverli al contrario. Esempio, calcoliamo 100 in binario:

• 100/2 = 50 (con resto 0)
• 50/2 = 25 (con resto 0)
• 25/2 = 12 (con resto 1)
• 12/2 = 6 (con resto 0)
• 6/2 = 3 (con resto 0)
• 3/2 = 1 (con resto 1)
• 1/2 = 0 (con resto 1)

Il numero binario è 1100100

SOMMA BINARIA

L'addizione tra due o più numeri binari è analoga a quella riferita ai numeri decimali. La regola applicata in questo caso è la seguente :

• 0+0=0
• 0+1=1
• 1+0=1
• 1+1=0 con riporto di 1 alla colonna verso sinistra

Quando si ha un riporto si aggiunge 1 sulla colonna di sinistra (quella più significativa) e si procede rispettando la regola della somma.

011+ 110 1001 1 + 0 = 1 con riporto di 0 V 1 + 1 + 0 (di riporto) = 0 con 1 di riporto V 0 + 1 + 1 (di riporto) = 0 con 1 di riporto riporto finale

SOTTRAZIONE BINARIA

La sottrazione nel sistema binario si svolge nel modo seguente:

• 0-0=0
• 0-1=1 con prestito di 1 dalla colonna a sinistra
• 1-0=1
• 1-1=0

Quando si ha un prestito si sottrae 1 dalla colonna di sinistra (quella più significativa) e si procede rispettando la regola della differenza. Se sulla colonna di sinistra non si può concedere il prestito perché la cifra è 0, esso si trascina alla colonna successiva verso sinistra finché non si restituisce il prestito.

100- 010 010 / 0 - 0 = 0 (senza prestito) 0 - 1 (impossibile) -> 10 - 1 = 1 (1 di prestito) 1 -1 (di prestito) - 0 = 0

MOLTIPLICAZIONE BINARIA

La regola del prodotto binario segue esattamente quella della moltiplicazione di due numeri decimali. Infatti si ha:

• 0 x 0=0
• 0 x 1=0
• 1 × 0=0
• 1 x 1=1

1 01 X 1 1 0 = 000 + 101 × 0 1 0 1 + ->101 ×1 101 = ->101 × 1 11110

BIT

Il bit (b) rappresenta l'unità di definizione di uno stato logico, definito anche unità elementare dell'informazione trattata da un elaboratore. Le ragioni di questa scelta sono molto semplici. Lo stato "zero" e "uno" possono essere realizzati con la presenza o l'assenza di tensione elettrica ( impulso elettrico ) in un circuito. La rappresentazione logica del bit è rappresentata dai soli valori {0, 1}.

01010011 1 0 t

BYTE

Ai fini della programmazione è comune raggruppare sequenze di bit in entità più vaste che possono assumere valori in intervalli assai più ampi di quello consentito da un singolo bit. Questi raggruppamenti contengono generalmente un numero di stringhe binarie pari a una potenza binaria, pari cioè a 2^n (dove n è la lunghezza della stringa) . Il più noto gruppo di bit è il byte (B), corrispondente a 8 bit, che costituisce l'unità di misura più utilizzata in campo informatico. Un byte può contenere 256 informazioni perché 2^8=255 (da 0 a 255) .

bit 1 01 10001

UNITÀ DI MISURA BYTE

byte BYTE BYTE = 8 BITS KILOBYTE = 1.024 BYTES: 210 MEGABYTE= 1.049.576 BYTES: 220 GIGABYTE= 1.073.741.824 BYTES: 230 TERABYTE= 1.099.511.627.766 BYTES: 240 PETABYTE= 1.125.899.906.842.624 BYTES: 250 EXABYTE= 1.152.921.504.606.846.976 BYTES: 260 ZETTABYTE= 1.180-591.620.717.411.303.424 BYTES: 270 YOTTABYTE= 1.208.925.819.614.629.174.706.176 BYTES: 280

TRANSISTOR

Il transistor è un componente elettronico composto da tre terminali (tripolo) detti base, collettore ed emettitore. La base controlla il flusso della corrente tra collettore ed emettitore. Il verso della corrente è indicato da una freccia. E' un semiconduttore (I semiconduttori, nella scienza e tecnologia dei materiali, sono materiali, appartenenti alla categoria dei semimetalli, che possono assumere una resistività superiore a quella dei conduttori e inferiore a quella degli isolanti. Essi sono alla base di tutti i principali dispositivi elettronici) usato nei circuiti analogici e digitali.

collettore base 11 emettitore

FUNZIONAMENTO DEL TRANSISTOR

Se la base riceve una tensione in ingresso superiore a una tensione di soglia (ad esempio V_IN 0.6 Volts), il transistor lascia passare la corrente tra collettore ed emettitore. Viceversa, la blocca. Un transistor si comporta come un interruttore pilotato dalla tensione.

Basis Kollektor A Emitter Etwas Basisstrom kann fließen; Der Transistor schaltet durch.

TRANSISTOR ON

La base riceve una tensione in ingresso superiore alla tensione di soglia. Tra C e E passa corrente.

i i ON c c ₿ V __= 0.2V CE E DIE E DIE IN circuito equivalente

TRANSISTOR OFF

La base riceve una tensione in ingresso inferiore alla tensione di soglia. Tra C e E non passa corrente (circuito aperto) .

1 1 OFF C Č C B i= 0 E O E DIE circuito equivalente

EVOLUZIONE DEL TRANSISTOR

Per questo motivo, per esempio, le radio fino agli anni '50 del Novecento erano dispositivi enormi. Negli anni '60 i transistor sostituirono le valvole e le radio divennero dispositivi portatili. Nacque così l'elettronica. La diffusione del transistor consenti la miniaturizzazione dei circuiti. A sua volta la miniaturizzazione permise di aumentare la frequenza della corrente nei circuiti grazie al principio di quasi stazionarietà. In conclusione, con l'arrivo del transistor i dispositivi elettronici divennero più piccoli e più veloci ad elaborare i segnali.

vecchia radio a valvole (anni '40-'50) fonte immarini Pivahav radio a transistor (anni '60-'70) WWW.AMADEAMIMINI ARALOGICA BOOLEANA

ALGEBRA BOOLEANA

I computer operano con segnali elettrici con valori di potenziale discreti:

• sono considerati significativi soltanto due potenziali (high/low)
• i potenziali intermedi, che si verificano durante le transizioni di potenziale, non vengono considerati.

L'aritmetica binaria è stata adottata proprio perché i bit sono rappresentabili naturalmente tramite elementi elettronici in cui siamo in grado di distinguere i 2 stati del potenziale elettrico (high/low) . Il funzionamento dei circuiti elettronici può essere modellato tramite l'Algebra di Boole. solo 2 valori: valore logico True (1) => livello di potenziale alto valore logico Falso (0) => livello di potenziale basso

ALGEBRA DI BOOLE

L'algebra di Boole (anche detta algebra booleana o reticolo booleano), in matematica e logica matematica, è il ramo dell'algebra in cui le variabili possono assumere solamente i valori vero e falso (valori di verità), generalmente denotati rispettivamente come 1 e 0. Le operazioni fondamentali non sono addizione e sottrazione ma gli operatori logici. Le tabelle della verità (o tabelle logiche) sono tabelle usate nella logica per determinare se, attribuiti i valori di verità alle proposizioni che la compongono, una determinata proposizione è vera o falsa. La tabella di verità quindi si applica a qualsiasi operatore logico vero-funzionale, vale a dire in cui le condizioni di verità o falsità di qualunque enunciato che si ottiene applicando quell'operatore è determinato interamente ed esclusivamente da quelle degli enunciati più semplici a cui si applica.

xyz (x Ay) V (xAz) V (yAz) FFF F FF V F FVF F FV V V VFF F VFV V VVF V VVV V

CONNETTIVI LOGICI

Un connettivo logico o operatore logico (nel contesto dell'algebra di Boole, i connettivi logici sono detti anche operatori booleani), è un elemento grammaticale di collegamento che instaura fra due proposizioni A e B una qualche relazione che dia origine ad una terza proposizione C con un valore vero o falso, in base ai valori delle due proposizioni fattori ed al carattere del connettivo utilizzato.

AND OR XOR NOT A - A XOR B B

OPERATORE NOT

La relazione di negazione NOT (-A) è un connettivo logico, attraverso il quale, a partire da una preposizione A si forma una nuova proposizione chiamata negazione di -A: la quale è vera quando A è falsa, ed è falsa quando A è vera. La relazione è così definita:

A A F V V F NOT NO

PORTA NOT CON TRANSISTOR

Come si sviluppa una porta not in un transistor? Se il transistor riceve 1, l'output va all'emettitore e quindi V_out va a 0. Se il transistor riceve 0, l'output va al collettore e V_out va a 1 (faremo solo questo esempio, non siamo ad un corso di elettronica) .

+Vcc NOT - Collector Vout Vin Base Emitter (a)