Architetture e Programmazione di Controllori Industriali con Antitrasformate

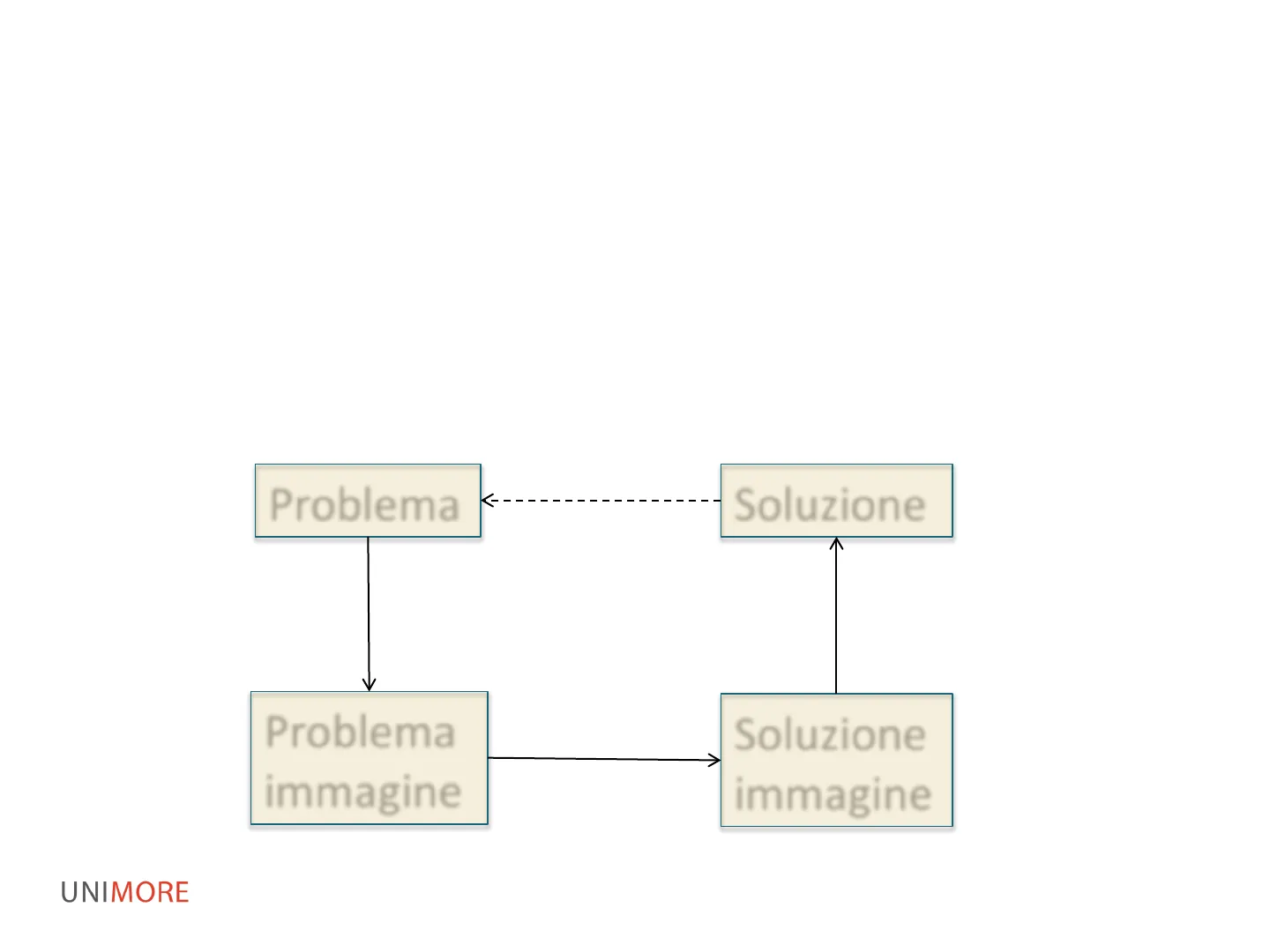
Antitrasformate Trasformata di Laplace

Recap

Mediante la trasformazione di Laplace un'equazione differenziale nel dominio del tempo si trasforma in un'equazione algebrica, di più semplice soluzione, nel dominio complesso.

Problema Soluzione Trasformata di Laplace Antitrasformata di Laplace Problema immagine Soluzione immagine

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 2

Trasformata di Laplace

Dal dominio complesso a quello temporale

Dove: [ [f(t)] a+jT f(t) = 1 1 lim 2Tf T->0 'a-jT F (s) eST ds f(t) F(s) C-1 [F(s)] è utile vincolare gli ingressi considerando solo alcune classi di segnali

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 3

Trasformata di Laplace

Dal dominio complesso a quello temporale

La determinazione della risposta in evoluzione libera e della risposta forzata di un sistema lineare e stazionario, nel dominio del tempo, si può ottenere mediante l'antitrasformata delle funzioni:

Zfo bi si Y(s) = i=0 i=o aisi U(s) + Et oai Σ'osiy(i-i-1) (0) i=0 Evoluzione forzata Evoluzione libera

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 4

Trasformata di Laplace

Antitrasformata di funzioni razionali

Considerando il termine Efobi si U(s) Possiamo considerare U (s) come rapporto di polinomi in s se u(t) è un ingresso canonico. Allora l'antitrasformata sarà del tipo:

n! L[tne-at] = (s + a)n+1

UNIMORE 19/10/2023 Architetture e Programmazione di Controllori Industriali 5

Trasformata di Laplace

Antitrasformata di funzioni razionali

Mentre il termine Li-o ai Zizo sjy(i-j-1) (0-) i=0 È un rapporto di polinomi in s ,dividendo numeratore e denominatore per a =1, si ha:

F (s) = P(s) Q(s) = bmsm + bm-1sm-1 + ... + bis + bo m-1 sn + an-isn-1 + ... + as + ao Ossia funzioni razionali fratte.

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 6

Trasformata di Laplace

Segnali canonici

La trasformata di Laplace dei segnali canonici è data dal rapporto si due polinomi, di conseguenza l'uscita è data dal rapporto di due polinomi.

Y(s) = F (s)U(s)

F(s)	f(t)
1	8(t) (impulso unitario in t = 0)
1	S
1	tu(t) (funzione rampa)
1	1
n-1	(n-1)!
1	-as
u(t-a) (gradino unitario in t = a)	S
1	1
1	1
s+a'	1+ts
T	1
1	1
1	1
m-le	(sta)n'
(1 +ts)"	(n-1)!
T" (n-1)!	1
1	1
-(1-e-ª1),	1-e-
1	1
(e " - e br)	(s+a) (s+b)
b-a	1
(e +1 - e +2)	(1 +[]s) (1+t2s)
1	(α-a)e at - (a-b)e bt)
(s+a) (s+b)	b-a
1+Ts	1
1	1
(1 +T1s) (1+[2s)	τι - τ2
3	sen ot
$2+@02	S
cos @t	$2+ 002

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 7

eur , -e i s (s+a)' s(1+ts) 1 tn-Ip-at u(t) (gradino unitario in t = 0) $2

Antitrasformata di Laplace

Funzioni razionali fratte

F (s) = P(s) Q(s) = bmsm + bm-1S m-1 + ... + bis + bo sn + an-1sn-1 + ... + ans + ao n-1 La differenza n-m tra il grado del polinomio al denominatore e il grado del polinomio al numeratore è detta grado relativo di F(s).

• Funzioni razionali fratte con un grado relativo negativo corrispondono a sistemi o segnali anticipativi fisicamente non realizzabili.

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 8

Antitrasformata di Laplace

Funzioni razionali fratte

Data una funzione razionale fratta:

F (s) = P(s) Q (s) L'equazione: $(s) = s" + an-1sn-1 + ... + ans + ao=0 E detta equazione caratteristica di F (s) la quale ha: p1, P2, ... , Pa radici reali o complesse (coppie coniugate).

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 9

Antitrasformata di Laplace

Funzioni razionali fratte

Allora: $(s) = sn + an-1sn-1 + ... + a1s + ao Può essere scritta come: ¢(s)= (s-p1)(s-p2) ... (s-Pn) P(s) F(s) = Q(s) È possibile scrive F(s) in forma fattorizzata:

F(s) = P(s) Q(s) = K (s-Z1)(s-Z2) ... (s - Zn) (s-p1)(s-p2) ... (s -Pn) Dove K è un opportuno guadagno.

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 10

Antitrasformata di Laplace

Funzioni razionali fratte

• Le radici:Z1, Z2, ... , Zn di P (s) sono dette ZERI di F (s).
• Le radici:p1, P2, ... , Pn di Q (s) sono detti POLI di F (s).
• Una funzione razionale è completamente determinata, a meno di un fattore costante K, una volta assegnati i suoi zeri e i suoi poli.

UNIMORE 19/10/2023 Architetture e Programmazione di Controllori Industriali 11

Antitrasformata di Laplace

Funzioni razionali fratte: esempi

F(s) = 2s+4 s2+4s+3 2(s+2) = (s+1)(s+3) Zeri: z = - 2 Poli: p1 = - 1, p2 =- 3

F(s) = s2+6s+5 s3+2s2+16s (s+1)(S+5) - s(s+1+jv15)(s+1-jv15) Zeri:z1 =- 1, z1 =- 5 Poli: p1 = 0, p2 = - 1- jv15, P2 = - 1+ jv15

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 12

Antitrasformata di Laplace

Funzioni razionali fratte

Se F(s) è una funzione razionale fratta strettamente propria (cioè il grado relativo > 0: il grado del polinomio a numeratore è inferiore a quello del denominatore. Si può, una volta calcolate le n radici del polinomio al denominatore, scomporre il rapporto di polinomi in una somma di n termini aventi a numeratore una costante e a denominatore un fattore binomio in s (fratti semplici o frazioni parziali), che risultano facilmente antitrasformabili:

F(s) = P(s) = Q(s) (s-p1)(s-p2) ... (s -Pn) P(s) Non è necessario calcolare le radici del numeratore!

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 13

Antitrasformata di Laplace

Funzioni razionali fratte

P(s) F (s) = P(s) = Q(s) (s-P1)(s-p2) ... (s - Pn) Per antitrasformare F(s) si possono avere due casi:

• Tutti i poli sono semplici, ossia pi = p;, per ogni coppia di indici i e j (molteplicità = 1).
• Vi sono poli multipli, ossia esiste almeno una coppia di indici i e j per i quali si ha pi = Pi (molteplicità > 1).

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 14

Antitrasformata di Laplace

Residui

Lo sviluppo della funzione F(s) in fratti semplici nel caso di poli tutti distinti porta alla seguente relazione

P(s) P(s) i=1 n Ri F (S) = Q(S) = (s-P1)(s -p2) ... (s - Pn) = S - Pi nella quale le costanti R;, ciascuna relativa al polo pi, sono dette residui, e sono:

• reali, in corrispondenza a poli reali;
• a coppie complesse coniugate in corrispondenza di coppie di poli complessi coniugati.

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 15

Antitrasformata di Laplace

Poli semplici calcolo dei residui

R¡ è il residuo associato al polo pi (i=1, ... ,n)

Ri = ( s - pi ) P(s) Q(s) S=Pi P(Pi) Ri = (Pi - P1) (Pi - P2) ... (pi - Pi-1) (Pi - Pi+1) ... (Pi - Pn)

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 16

Antitrasformata di Laplace

Poli semplici calcolo dei residui

Essendo:

n F (s) = Ri s - Pi i=1 E anche: L-1 = s - a. 1 eat - la funzione F(s) si antitrasforma, se posta in forma di fratti semplici:

f(t) = > RiePit i=1 n J

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 17

Antitrasformata di Laplace

Esempio

Sia F(s) = 5s+3 (s+1)(s+3)s(+2) K (s+1) + (s+2) + K3 K2 (s+3) Allora i residui saranno:

K2= = 7 (s =- 2) K3= 5(-2)+3 (-2+1)(-2+3) 5(-3)+3 =- 6 (s =- 3) F (s) = -1 (s+1) + (s+2) 7 (s+3) 6 Essendo l'antitrasformata: [-1 1 = eat s-a f(t) =- e-t + 7e-2t - 6e-3t

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 18

K1 = (-3+1)(-3+2) 5(-1)+3 (-1+3)(-1+2) =- 1 (s =- 1)

Antitrasformata di Laplace

Esempio

5s+3 F(s) = (s+1)(s+3)s(+2) f(t) =- e-t + 70-2t - 6e -3t

f(t) 0.7 0.6 0.5 0.4 ₴ 0.3 0.2 0.1 0 -0.1 0 2 4 6 8 10 Tempo (sec)

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 19

Antitrasformata di Laplace

Poli complessi coniugati

Dalla formula di Eulero: eil = cos(0) + i sin(0) Se nella funzione F (s) sono presenti coppie di poli complessi coniugati, nella sua antitrasformata vi saranno coppie di esponenziali complessi, moltiplicate per coefficienti ossia i residui, anche essi complessi coniugati.

• Applicando la formula di Eulero, si possono ridurre le coppie di esponenziali complessi ad esponenziali reali moltiplicati per funzioni trigonometriche.

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 20

Antitrasformata di Laplace

Poli complessi coniugati

Consideriamo, per semplicità, una funzione F(s) del tipo:

F(s) = s2 + as + ao 1 dove a1 e ao sono tali da dare luogo ad una coppia di poli complessi coniugati P1 = Oi + jWi, P2 = Oi - jWi = p ∗ I relativi residui sono anche essi complessi coniugati R1 = Ui + jvi, R2 = Ui - jvi = R1 ∗

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 21

Antitrasformata di Laplace

Poli complessi coniugati

Allora F(s) può essere scritta:

F(s) = R1 1 + R 2 S - P2 * R 1 S - P1 S- P1 + s - P1 * s-ơi-jwi 1 ui+jVi Ui-jvi + s-oi+jwi R Utilizzando la formula di Eulero: uitjvi = pele p = Vu, 2+ 0,2 0 = arctan ui Vi

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 22

Antitrasformata di Laplace

Poli complessi coniugati

Allora F(s) può essere scritta:

F (s) = Ui+jvi s-oi-jWi + Ui-jvi s-oi+jwi = p ej0 s-ơi-jWi + s-oi+jwi e-je Ricordando che L-1 1 = eat s-a cos(s) = ejs + e-js 2 Antitrasformando: f(t) = p(eit+j(w;+0) + e it-j(W;+0) = 2peitcos(W; +0)

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 23

Antitrasformata di Laplace

Esempio: Poli complessi coniugati

F(s) = 7s2 -8s + 5 s3 + 2s2 + 5s 7s2-8s+5 = R1 + R2 S+1-2j + R2* S+1+2j _= 1 S = = + 1 3+j4 S+1-2j S+1+2j Allora: p = 5 0 = arctan 4 3 4 f(t) = 1+10e-tcos |2t + arctan(2)

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 24

+ 3-j4 s3+s2+5s S

Antitrasformata di Laplace

Esempio: Poli complessi coniugati

f(t) = 1 + 10e-tcos 4 2t + arctan ) 3

f(t) 7 6 5 4 3 f(t) 2 1 0 -1 -2 -3 0 2 4 6 8 10 Tempo (sec)

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 25

Antitrasformata di Laplace

Poli complessi coniugati: recap

• Una funziona razionale fratta F(s), e quindi nel caso di interesse una funzione di trasferimento, è esprimibile sempre come rapporto di due polinomi.
• Nell'ipotesi che le radici del polinomio a denominatore presentino molteplicità pari a uno, una volta che la F(s) sia stata decomposta in fratti semplici, da luogo ad espressioni del tipo:

F(s) =- + R S i=1 K s - Pi Ri + ui + jvi i=1 l S - oi - jwi + S- Ơi + jWi Ui - jvi

UNIMORE 16/10/2023 Architetture e Programmazione di Controllori Industriali 26