Cerchio e circonferenza: definizioni e proprietà in matematica per la scuola superiore

Cerchio e Circonferenza: Definizioni

Cerchio e circonferenzaLe definizioni di circonferenza e cerchio

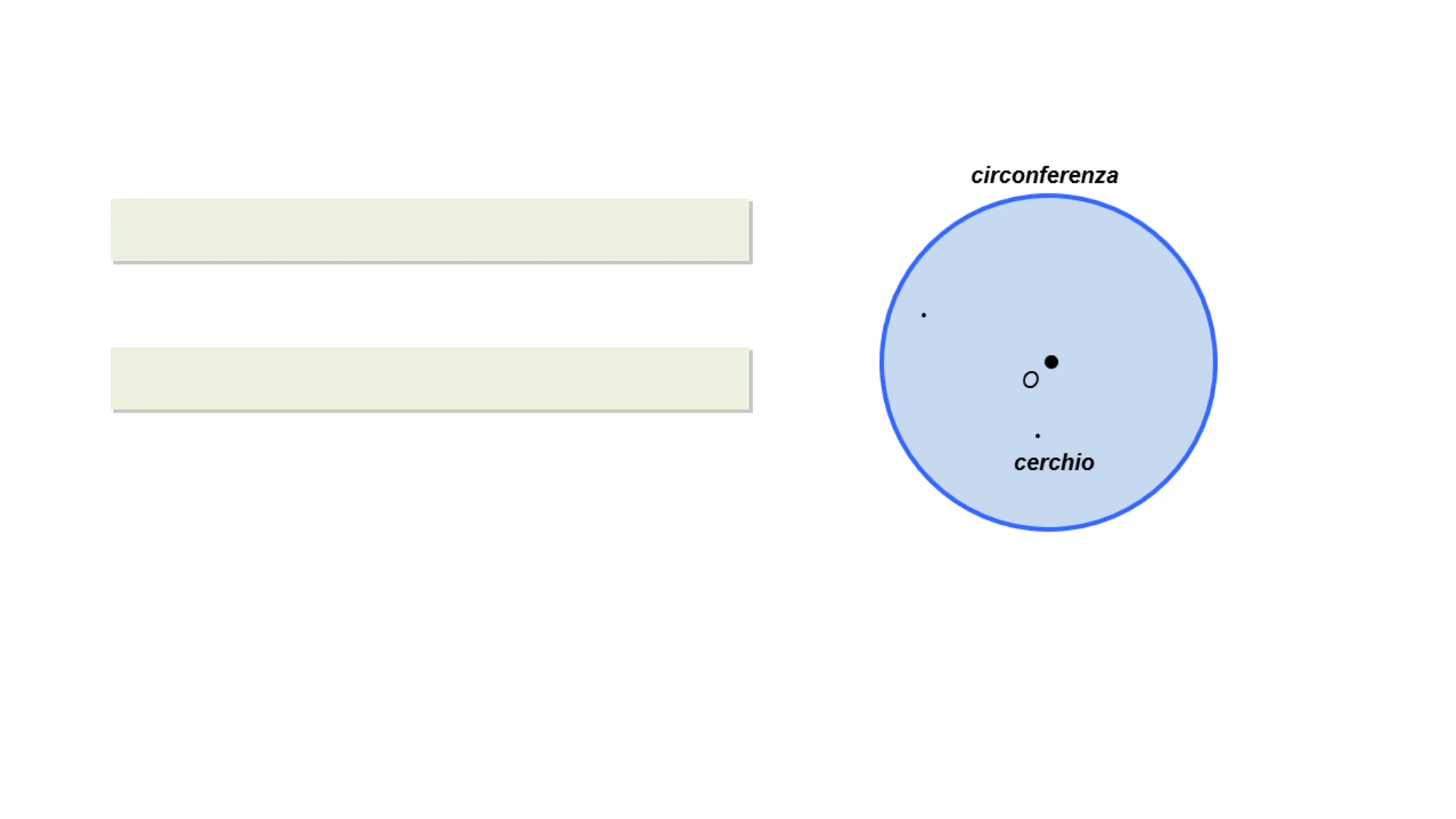
DEFINIZIONE. La circonferenza è l'insieme di tutti e soli i punti di un piano equidistanti da un punto fisso detto centro.

DEFINIZIONE. Il cerchio è la parte di piano costituita dalla circonferenza e dai punti ad essa interni.

circonferenza C cerchioparti di una circonferenza

Arco e Corda

DEFINIZIONE. Presi due punti A e B su una circonferenza, si chiama ARCO ciascuna delle due parti in cui la circonferenza viene divisa; lo si indica con la scrittura: AB I due punti scelti sulla circonferenza vengono detti estremi dell'arco.

DEFINIZIONE. Si dice corda di una circonferenza ogni segmento che abbia gli estremi appartenenti alla circonferenza.

A O B arco corda B A O

Diametro e Semicerchio

DEFINIZIONE. Si dice diametro di una circonferenza ogni corda passante per il centro della circonferenza. Esso divide il cerchio in due parti congruenti dette semicerchi. Gli estremi di un diametro dividono una circonferenza in due semicirconferenze.

PROPRIETÀ. I diametri di una circonferenza sono tutti fra loro congruenti; in particolare d = 2 . r.

semicirconferenza diametro B A O semicerchio

Proprietà della Circonferenza

Perpendicolare a una Corda

PROPRIETÀ. La perpendicolare condotta dal centro di una circonferenza ad una corda divide tale corda a metà.

PROPRIETÀ. La perpendicolare ad una corda nel suo punto medio (asse della corda) passa per il centro della circonferenza.

B M O A

Archi e Corde Congruenti

LE PROPRIETÀ DELLA CIRCONFERENZA PROPRIETÀ. In una stessa circonferenza ad archi congruenti corrispondono corde congruenti e viceversa.

A C O B H D

Distanza delle Corde dal Centro

LE PROPRIETÀ DELLA CIRCONFERENZA TEOREMA. Due corde congruenti di una stessa circonferenza hanno la stessa distanza dal centro.

A B H O C D

Parti di un Cerchio

Settore Circolare

PARTI DI UN CERCHIO : settore circolare DEFINIZIONE. Si chiama settore circolare ognuna delle due parti in cui un cerchio è diviso da due suoi raggi.

settore O B A settore

Segmento Circolare a una Base

PARTI DI UN CERCHIO : segmento circolare a UNA BASE DEFINIZIONE. Si chiama segmento circolare a una base ognuna delle due parti in cui un cerchio è diviso da una sua corda.

segmento circolare A B · C segmento circolare

Segmento Circolare a Due Basi

PARTI DI UN CERCHIO : segmento circolare a DUE BASI DEFINIZIONE. Si chiama segmento circolare a due basi la parte di cerchio compresa fra due corde parallele. La distanza fra le due basi si chiama altezza.

A B segmento circolare altezza C D

Posizioni di una Retta rispetto a una Circonferenza

Retta Esterna

POSIZIONI DI UNA RETTA RISPETTO AD UNA CIRCONFERENZA : RETTA ESTERNA 1. Primo caso OP > r DEFINIZIONE. Una retta è esterna ad una circonferenza se non ha con essa alcun punto in comune.

S r O . P

Retta Tangente

POSIZIONI DI UNA RETTA RISPETTO AD UNA CIRCONFERENZA : RETTA TANGENTE 2. Secondo caso OP = r DEFINIZIONE. Una retta è tangente ad una circonferenza se ha un SOLO PUNTO in comune con essa. Tale punto è detto punto di tangenza.

PROPRIETÀ. La tangente ad una circonferenza è sempre perpendicolare al raggio nel punto di tangenza.

S r 0 . L P

Retta Secante

POSIZIONI DI UNA RETTA RISPETTO AD UNA CIRCONFERENZA : RETTA SECANTE 3. Terzo caso OP

I S A r P B

Tangenti da un Punto Esterno

PROPRIETÀ. Se da un punto esterno ad una circonferenza conduciamo le TANGENTI alla circonferenza, otteniamo due segmenti di tangente tra loro congruenti.

PROPRIETÀ. La semiretta che congiunge il punto esterno con il centro della circonferenza è BISETTRICE DELL'ANGOLO formato dalle due tangenti stesse.

T1 H P T2 -

Posizioni di Due Circonferenze

Circonferenze Esterne

POSIZIONI DI DUE CIRCONFERENZE : circonferenze ESTERNE 1. Primo caso DEFINIZIONE. Due circonferenze si dicono esterne l'una all'altra se la distanza dei loro centri è maggiore della somma dei loro raggi:

00'>r+r'

r r' O

Circonferenze Tangenti Esternamente

POSIZIONI DI DUE CIRCONFERENZE : tangenti esternamente 2. Secondo caso DEFINIZIONE. Due circonferenze sono tangenti esternamente se la distanza dei loro centri è congruente alla somma dei loro raggi:

00'=r+r'

r Pr' O O'

Circonferenze Tangenti Internamente

POSIZIONI DI DUE CIRCONFERENZE : tangenti internamente 3. Terzo caso DEFINIZIONE. Due circonferenze sono tangenti internamente se la distanza dei loro centri è congruente alla differenza dei loro raggi:

00'=r-r'

rr A

Circonferenze Secanti

POSIZIONI DI DUE CIRCONFERENZE : ciconferenze secanti 4. Quarto caso DEFINIZIONE. Due circonferenze si dicono secanti se la distanza dei loro centri è minore della somma dei loro raggi e maggiore della loro differenza:

00'r-r'

A 1 O r B

Circonferenze Interne e Concentriche

POSIZIONI DI DUE CIRCONFERENZE : ciconferenze INTERNE 5. Quinto caso DEFINIZIONE. Due circonferenze si dicono una interna all'altra se la distanza dei loro centri è minore della differenza dei loro raggi:

00'

DEFINIZIONE. Due circonferenze si dicono CONCENTRICHE se hanno lo stesso centro.

DEFINIZIONE. Si chiama CORONA CIRCOLARE la parte di piano delimitata da due circonferenze concentriche di raggi disuguali.

r r'

Angoli al Centro

Angoli al centro DEFINIZIONE. Si chiama ANGOLO AL CENTRO di una circonferenza ogni angolo avente il vertice nel suo centro.

A B D C A O B

PROPRIETÀ. Angoli al centro congruenti insistono su archi congruenti e, viceversa, ad archi congruenti corrispondono angoli al centro congruenti.

Angoli alla Circonferenza

Tipi di Angoli alla Circonferenza

Angoli alla circonferenza DEFINIZIONE. Si chiama angolo alla circonferenza un angolo convesso con il vertice su di essa e: · entrambi i lati secanti · un lato secante e uno tangente · entrambi i lati tangenti alla circonferenza

P A entrambi i lati secanti C B A=P un lato secante e uno tangente · O B A=P=B entrambi i lati tangenti alla circonferenza O

Proprietà degli Angoli alla Circonferenza

Angoli al centro e alla circonferenza : proprietà PROPRIETÀ. Ad ogni angolo alla circonferenza corrisponde un solo arco sul quale insiste; viceversa, ad ogni arco corrispondono infiniti angoli alla circonferenza.

A P Q R S B

Relazione tra Angoli al Centro e alla Circonferenza

Teorema Fondamentale

Relazione tra angoli al centro e angoli alla circonferenza TEOREMA. Ogni angolo alla circonferenza è la metà del corrispondente angolo al centro.

P A B Q R P B A

Angoli Congruenti sullo Stesso Arco

PROPRIETÀ. Tutti gli angoli alla circonferenza che insistono su uno stesso arco sono fra loro congruenti.

Proprietà Aggiuntive degli Angoli

Angolo su Semicirconferenza

angoli al centro e alla circonferenza : proprietà PROPRIETÀ. Ogni angolo alla circonferenza che insiste su una semicirconferenza è retto.

Triangoli Rettangoli e Mediana

PROPRIETÀ. Tutti i triangoli aventi un vertice sulla circonferenza e un lato coincidente con il diametro sono triangoli rettangoli.

PROPRIETÀ. In ogni triangolo rettangolo la mediana relativa all'ipotenusa è congruente alla metà dell'ipotenusa stessa.

P B A