Altre tipologie di mutazioni genetiche: anomalie cromosomiche

Altre tipologie di mutazioni

Le sostituzioni di un singolo nucleotide giocano un ruolo fondamentale nella creazione della variabilità ALLELICA, tuttavia esistono altre tipologie di mutazioni che hanno giocato un ruolo molto importante durante l'evoluzione. Si tratta delle ANOMALIE CROMOSOMICHE, ovvero anomalie che coinvolgono un frammento più o meno lungo di un cromosoma o più cromosomi. La nascita di nuovi GENI nel processo evolutivo si origina spesso da questi processi.

Esistono diverse tipologie di ANOMALIE CROMOSOMICHE.

pietro.parma@unimi.itLe anomalie cromosomiche

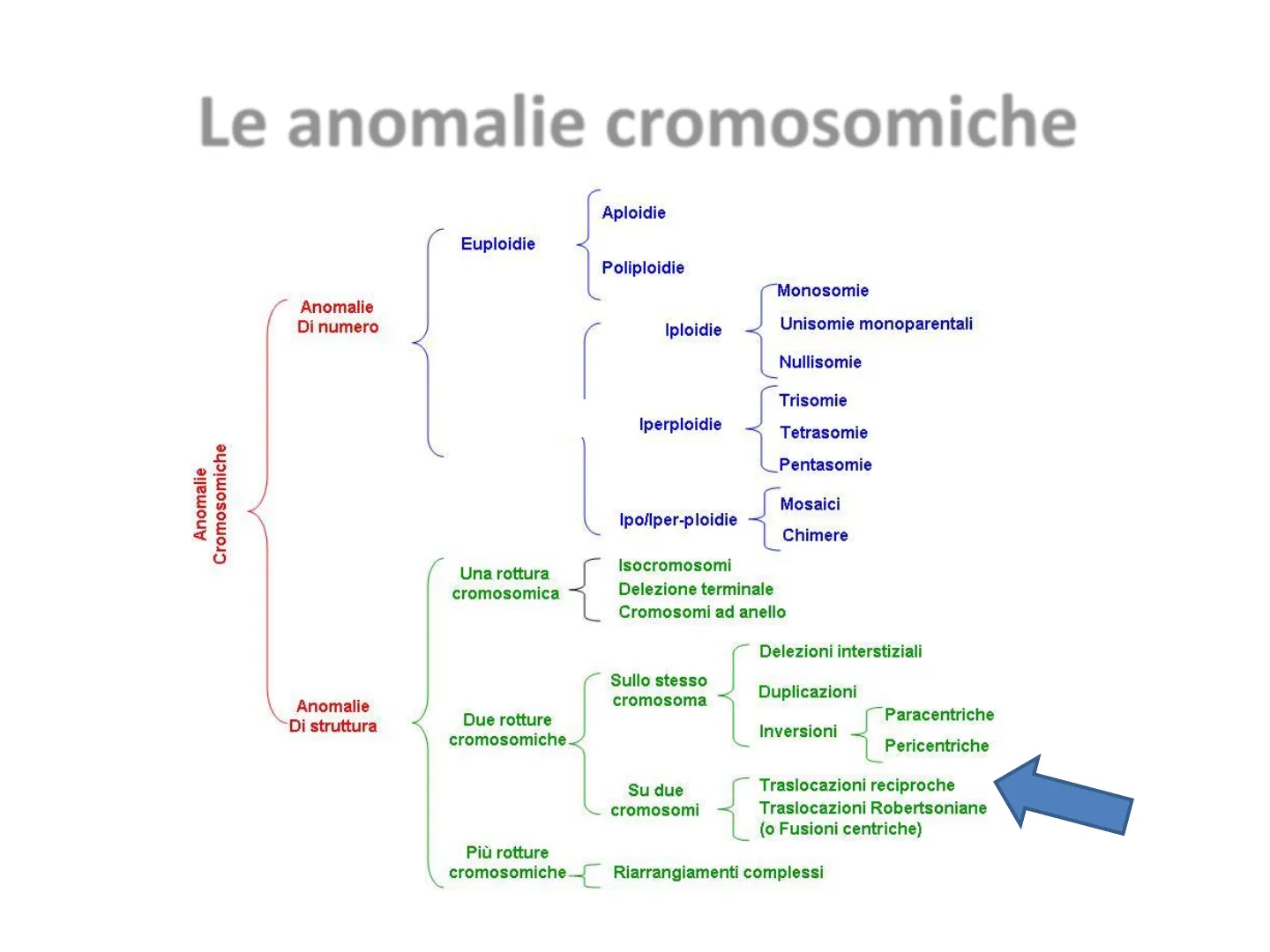
Anomalie di numero

• Aploidie
• Euploidie
• Poliploidie
• Monosomie
• Unisomie monoparentali
• Iploidie
• Nullisomie
• Trisomie
• Aneuploidie
• Iperploidie
• Tetrasomie
• Pentasomie

Anomalie Cromosomiche

• Ipo/lper-ploidie
• Mosaici
• Chimere

Anomalie di struttura

Una rottura cromosomica

• Isocromosomi
• Delezione terminale
• Cromosomi ad anello

Due rotture cromosomiche

Delezioni interstiziali

Sullo stesso cromosoma

• Duplicazioni
• Inversioni
• Paracentriche
• Pericentriche

Su due cromosomi

• Traslocazioni reciproche
• Traslocazioni Robertsoniane (o Fusioni centriche)

Più rotture cromosomiche

• Riarrangiamenti complessi

pietro.parma@unimi.itLe traslocazioni reciproche

Abbiamo visto in precedenza che i gei sono composti da regioni che codificheranno per un polipetide (gli esoni) e da regioni che invece sono escluse da questo processo (introni). Nelle TRASLOCAZIONI RECIPROCHE due cromosomi NON OMOLOGHI si scambiano dei frammenti e quindi si ha una ricombinazione genica.

pietro.parma@unimi.itLe traslocazioni reciproche

ATG TGA ATG TGA ATG TGA ATG TGA Nuovo gene ?

pietro.parma@unimi.itCytogenetics of Livestoks

Corso Opzionale accessibile a tutti gli studenti 4 CFU I semestre

pietro.parma@unimi.itI caratteri quantitativi

I CARATTERI dei quali abbiamo analizzato le modalità di trasmissione e la loro infuelza sul FENOTIPO (piselli di Mendel, Drosophila di Morgan, persitenza del lattosio in età adulta, capacità di metabilizzare l'etanolo) sono tutti caratteri QUALITATIVI, ovvero caratteri che sono (nella maggior parte dei casi) MONOGENICI e che seguono le leggi di Mendel. Esiste però un'altra categoria di CARATTERI per i quali l'ESPRESSIONE FENOTIPICA non segue completamente le leggi di Mendel. Si tratta dei caratteri QUANTITATIVI o POLIGENICI. I caratteri QUANTITATIVI sono molto comuni sia nel campo vegetale che animale. Sono, per esempio, caratteri QUANTITATIVI: l'altezza al garrese, la produzione di latte, il contenuto di colesterolo nel sangue, il peso alla macellazione, etc.

pietro.parma@unimi.itI caratteri quantitativi

Caratteri QUALITATIVI

L'espressione FENOTIPICA di un carattere è regolato da un solo GENE.

Caratteri QUANTITATIVI

Fenotipo Genotipo Ambiente L'espressione FENOTIPICA di un carattere è regolato da PIU' GENI e dall'interazione con l'AMBIENTE.

Genotipo Fenotipo Ambiente

Genotipo Fenotipo AmbienteI caratteri quantitativi

Una caratteristica comune dei caratteri quantitativi è che i diversi FENOTIPI presenti per un carattere non sono facilmente separabili tra di loro tanto che spesso un fenotipo sfuma in un altro. Lo studio di questi caratteri è molto complesso e richiede strumenti diversi. Si tratta della GENETICA QUANTITATIVA. Dal punto di vista didattico affronteremo le problematiche principali.I caratteri quantitativi

Esempio di carattere quantitativo: colore dei chicchi di grano

Supponiamo che il carattere colore sia controllato da due geni e che ciascun allele dominante agisca in modo additivo per determinare il colore

P AABB aabb bianco rosso

F1 AbBb rosa

AB Ab aB ab

F2 AB AABB AABb AaBB AaBb

Ab AABb AAbb AaBb Aabb

aB AaBB AaBb aaBB aaBb

ab AaBb Aabb aaBb aabb

Numero alleli dominanti nella F2 Alleli progenie 0 1 1 4 2 6 3 4 4 1I caratteri quantitativi

Numero alleli dominanti nella F2 Alleli progenie 0 1 1 4 2 6 3 4 4 1

6/16 4/16 1/16 0 1 2 3 4 Rosso scuro Bianco A A a a P BB b b CC × CC A a F1 B b Rosso intermedio C c Distribuzione dei fenotipi nella F2

F 2 Frequenza di segregazione nella F2 2964 15/64 6/64 1/64- 6 5 4 3 2 1 0 Numero di alleli per la pigmentazione Quindi aumentando i numero di geni aumentano i FENOTIPI e la differenza tra i FENOTIPI diminuisci.I caratteri quantitativi

Nella maggior parte dei casi i FENOTIPI dei caratteri quantitativi, suddivisi in CLASSI, si distribuiscono secondo la curva NORMALE o curva di GAUSS.

Frequenza - 66% 95% 99% -3 -2 -1 +1 +2 +3 Media Deviazioni standard (s) dalla mediaLe proprietà della curva Gaussiana

Frequenza 66%- 95% 99% -3 -2 -1 +1 +2 +3 Media Deviazioni standard (s) dalla media La curva di Gauss possiede le seguenti proprietà: 1- è simmetrica rispetto al valore medio (u) 2- il valore medio corrisponde anche con la mediana e la moda 2- è asintotica all'asse delle X da entrambi i lati 3- possiede due punti di flesso (u+o) e (u-o) 4- L'area sotto la curva è pari a 1, essendo 1 la probabilità che un valore capiti tra - e +%La distribuzione normale

Frequenza 66% 95% -- 99% -3 £ -2 -1 +1 +2 +3 Media Deviazioni standard (s) dalla media Nella distribuzione normale il 66% dei campioni è compreso tra +-1 deviazione standard, il 95% è compreso tra +-2 deviazioni standard ed il 99% dei campioni è compreso tra +-3 deviazioni standard.La distribuzione normale

La forma e posizioine della distribuzione dipende da media e deviazione standard

Posizione (Ly) μ1 7 μ2 01= 02 Più a sinistra Più a destra 1 02 [l 2 x

1 Forma (o) 0102 μ1 = μ2 Meno variabile più variabile xLa distribuzione normale

I due paramentri fondamentali che definiscono la forma di una curva normale sono: - La media - La variabilità.

X = (Σ Χκ) n media

s2 = Σ (Χκ . Χ) 2 n - 1 varianza

S = Js2 Deviazione standardStima degli individui contenuti

Sapendo che un carattere, misurato in una popolazione, si distribuisce secondo la curva normale, è possibile prevedere il numero di soggetti presenti in un certo intervallo.

µ x

Z= μ-χ s = distanza dalla media espressa in rapporto alla deviazione standardStima degli individui contenuti

Area Z 0

Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

-3.4 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002

-3.3 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003

-3.2 0.0007 0.0007 0.0006 0.0006 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005

-3.1 0.0010 0.0009 0.0009 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007

-3.0 0.0013 0.0013 0.0013 0.0012 0.0012 0.0011 0.0011 0.0011 0.0010 0.0010

-2.9 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014 0.0019

-2.8 0.0026 0.0025 0.0024 0.0023 0.0023 0.0022 0.0021 0.0021 0.0020

-2.7 0.0035 0.0034 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026

-2.6 0.0047 0.0045 0.0044 0.0043 0.0041 0.0040 0.0039 0.0038 0.0037 0.0036 0.0048

-2.4 0.0082 0.0080 0.0078 0.0075 0.0073 0.0071 0.0069 0.0068 0.0066 0.0064 0.0084

-2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110 0.0143

-2.0 0.0228 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183

-1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233 0.0294

-1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367 0.0455

-1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559

-1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681

-1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823

-1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985

-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170

-1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611

-0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867

-0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148

-0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451

-0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.3264 0.2877 0.2843 0.2810 0.2776 0.3121

-0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483

-0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859

-0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247

-0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641

Z=1 0,1587 0,5-0,1587=0,3413 0,5 0,5+0,3413=0,8413

Z=2 0,0228 0,5-0,0228=0,4772 0,5 0,5+0,4772=0,9772

Z=1,35 0,0885 0,5-0,0885=0,4115 0,5 0,5+0,4115=0,9115

-2.5 0.0062 0.0060 0.0059 0.0057 0.0055 0.0054 0.0052 0.0051 0.0049

-2.3 0.0107 0.0104 0.0102 0.0099 0.0096 0.0094 0.0091 0.0089 0.0087

-2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146

-1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301

-1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0.0475 0.0465 0.1379

-0.9 0.1841 0.1814 0.1788 0.1762 0.3336 0.3300 0.3228 0.3192 0.3156

-0.4 0.3446 0.3409 0.3372 0.1469 0.1446 0.1423 0.1401Stima degli individui contenuti

Esempio: Stalla vacche da latte

Stalla vache da latte con 150 capi in lattazione Produzione media 35,2 + 7,1 lt/gg Se si vogliono eliminare tutte le bovine che producono meno di 27 lt/gg, quante bovine bisogna eliminare ?

Z= 35,2-27 = 1,15

Z £ 0

Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

-1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681

-1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823

-1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985

-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170

-1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379

-0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611

0 2119 0 2090 0 2061 0 20.33 0 2005 0 1977 0 1949 0 1922 0 1894 0 1867

Area 7,1 0,1251 150*0,1251= 18,7Altre distribuzioni

frequenza Weibull 0.025 0.020 valori MODA MEDIA 0.015 0.010 0.005 0.000 0 50 100 150 200La variabilità nei caratteri quantitativi

In un esempio precedente avevamo visto come il colore di una pianta, o di un fiore, può derivare dalla somma additiva di alleli appartenenti a diversi geni.

Però nei caratteri quantitativi la variabilità non è causata solo dai diversi genotipi presenti, ma anche dall'interazione con l'ambiente.

aabbccdd AaBbCcDd AABBccdd AABbCCdd AABBCCDD ...