Tecnologie informatiche: architettura dei sistemi di elaborazione e componenti hardware

Tecnologie Informatiche 2023/24

2023/24 Tecnologie informatiche PRIMA TL-CAT (VERS 0.2) PARTE 2 ANTONIO PINNA1 ISTITUTO DI ISTRUZIONE SUPERIORE polo "tecnico "G.M. DEVILLA" SASSARI

Introduzione ai Sistemi di Elaborazione

In questa seconda parte conosceremo come è realmente costruito internamente un sistema di elaborazione sia esso un personal computer o uno smartphone. Nelle lezioni precedenti abbiamo dato una prima distinzione in funzione della forma e dell'utilizzo, in questi ciclo di lezioni invece ci concentreremo su come è realmente costruito, se dovessimo fare un paragone con il mondo dei motori sino ad ora abbiamo capito che i mezzi di locomozione possono essere auto camion moto etc. adesso ci concentreremo sul motore la trasmissione, il cambio e così via.

Architetture dei Computer

Quello che ci si chiede è: come si definisce un computer? Tutti i dispositivi elettronici sono computer? A questo tipo di domande si risponde definendo esattamente come deve essere costruito un computer e quindi no un qualsiasi dispositivo elettronica non è un computer ma per esserlo deve rispettare l'architettura di Von Neumann.

Architettura di Von Neumann

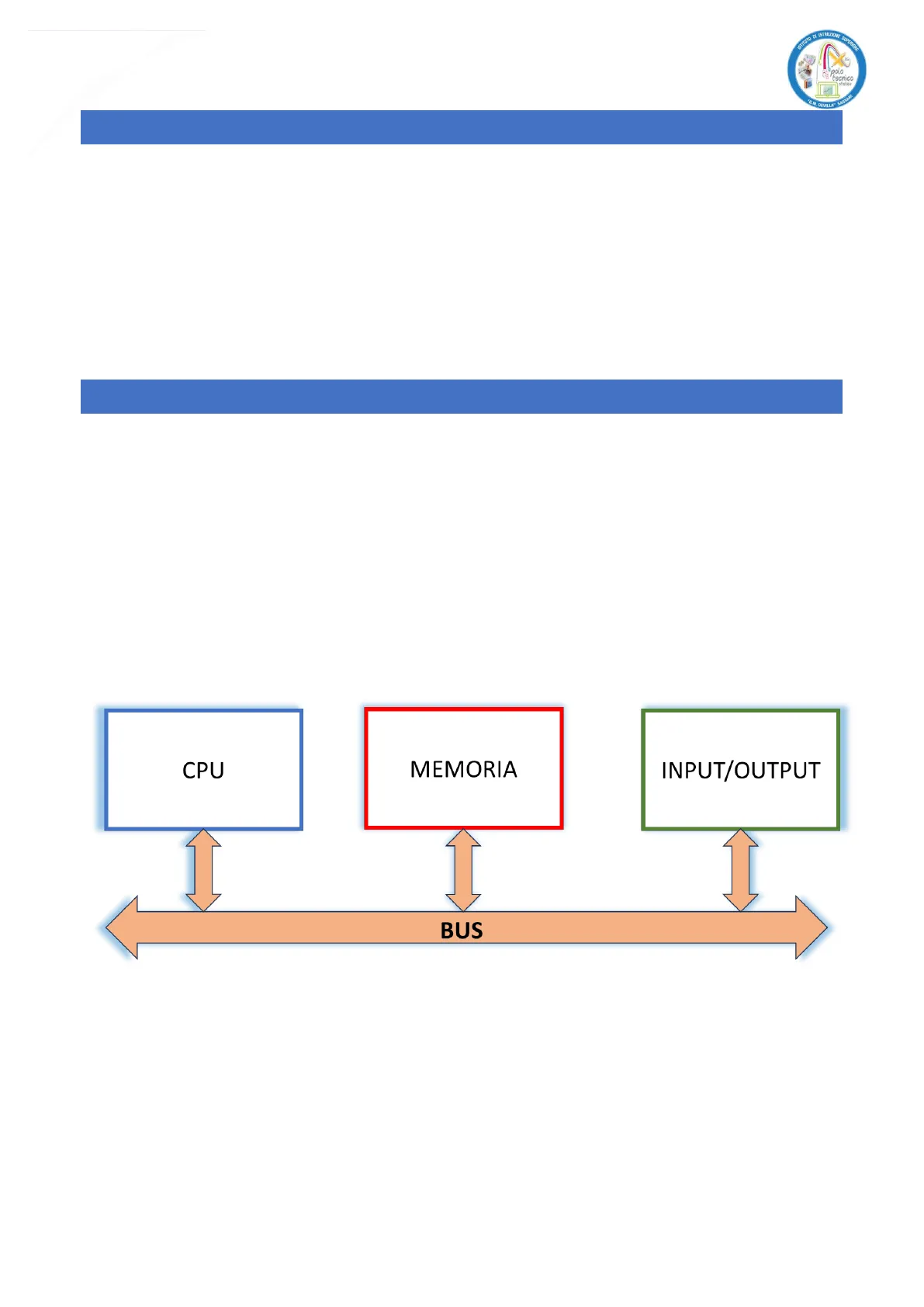
L'architettura li Von Neumann è illustrata nella seguente figura:

CPU MEMORIA INPUT/OUTPUT BUS

Affinché un dispositivo elettronica sia un sistema di elaborazione esso deve essere suddivisa nei seguenti componenti base

• CPU: è la parte che si occupa di interpretare ed eseguire le istruzioni e di eseguire i calcoli. È composta di celle elettroniche dette registri in cui vengono caricati i dati e dei circuiti per fare operazioni quali addizioni e moltiplicazioni.2 ISTITUTO DI ISTRUZIONE SUPERIORE polo "tecnico skatde "G.M. DEVILLA" SASSARI
• RAM: è la parte che si occupa di memorizzare le operazioni temporanee, viene detta anche RAM (Random Access Memory). Possiamo pensarla come un foglio di brutta sopra il quale uno studente, che rappresenta la CPU, annota i suoi calcoli
• Input/Output: sono tutte quelle componenti che servono per introdurre i dati e le istruzioni da elaborare e restituire o registrare i risultati ottenuti. Al tempo di Von Neumann l'input era costituito da una scheda perforata che conteneva il programma e l'output veniva stampato su un'apposita stampante. Oggi l'input è costituito dalla tastiera nel PC, dal touch nei Tablet e Smartphone; l'output è in genere il monitor o il disco fisso nel PC o anche la memoria flash dello smartphone dove sono registrati video, foto, e dove risiedono le app.
• Bus: essendo questi dispositivi elettronici, ovvero percorsi da correnti, servono dei fili per collegarli. Il bus è l'insieme di questi fili.

Architettura Harvard

Esiste una variabile della architettura di Von Neumann usata nei dispositivi portatili (ad esempio il decoder del segnale televisivo, oppure il chip che serve per poter trasmetter i dati in 5G o in Wi-Fi) che usano una variante della architettura vi Von Neumann, che prende il nome di architettura Harward.

Memory Data + Code Program Memory Data Memory Data Address CPU CPU Instruction address Variable address Data Devices 1/0 Devices Von Neumann Machine Harvard Machine

La differenza consiste nel fatto che i circuiti relativi ai dati sono separati da quelli relativi alle istruzioni.

Prima di approfondire ciascuna parte delle architetture andiamo a capire la lingua in cui parlano i computer.

Numeri Binari

Il sistema numerico binario è un sistema numerico posizionale in base 2. A differenza del sistema decimale (che è un sistema posizionale a base 10), che utilizza dieci cifre (da 0 a3 ISTITUTO DI ISTRUZIONE SUPERIORE polo "tecnico statale "G.M. DEVILLA" SASSARI 9), il sistema binario utilizza solo due simboli, di solito indicati con 0 e 1. Ogni numero espresso nel sistema numerico binario è definito "numero binario".

In informatica, il sistema binario è utilizzato per la rappresentazione interna dell'informazione dalla quasi totalità degli elaboratori elettronici. Questo perché le caratteristiche fisiche dei circuiti digitali rendono molto conveniente la gestione di due soli valori, rappresentati fisicamente da due diversi livelli di tensione elettrica. Questi valori assumono convenzionalmente il significato numerico di 0 e 1 o quelli di vero e falso della logica booleana.

Possiamo più banalmente pensare che noi esseri umani avendo dieci dita riusciamo a rappresentare 10 cifre, mentre i computer avendo a disposizione, all'interno dei loro circuiti, solo due valori: passa corrente e non passa corrente il metodo più naturale è quello in base 2.

Un numero binario è una sequenza di cifre binarie, come ogni numero che noi siamo abituati a trattare è una sequenza di cifre che vanno da 0 a 9.

Partiamo da un numero decimale così come noi lo conosciamo ad esempio 2375.

2 3 7 5 Numero 1 0 1 1 k h da u 1000 100 10 1 Peso Cifra 8 4 2 1 = 2x1000 + 3x100 + 7x10 + 5x1 = 2375 = 1x8 + 0x4 + 1x2 + 1x1 = 11 103 102 101 10º Peso Cifra come potenza della base 23 22 21 20 3 2 1 0 Posizione Cifra 3 2 1 0

Come risulta dalla figura il numero viene rappresentato in quattro posizioni o meglio in quattro celle, ad esempio analizziamo la cella verde delle centinaia il suo nome è h il valore è 100 o anche 102 e la posizione della cifra è 2 (assumendo la cifra delle unità è alla posizione 0) come è facile notare queste cifre darà contributo 3 centinaia ovvero 300 per il calcolo della cifra totale.4 ISTITUTO DI ISTRUZIONE SUPERIORE Spdo tecnico "G.M. DEVILLA" SASSARI

Adesso analizziamo a destra un altro numero ma stavolta espresso in binario 1011; la prima cosa che si nota è che nelle caselle posso solo rappresentare il numero 1 o lo 0, le altre cifre che usualmente conosciamo sono proibite.

Questa volta concentriamoci sul contributo dato dalla cifra di posizione 2 ovvero quella in rosso. Essendo cambiata la base di rappresentazione da 10 a 2 il valore in questa posizione sarà 2 e non 10! Questo perché in ogni posizione noi possiamo rappresentare solo 2 valori non 10! Pertanto se volessimo esprimerlo in decimale il contributo la calcolo del valore sarebbe 2.

Quindi come nel numero di destra se vogliamo trovare il valore il decimale del numero 1011 dobbiamo moltiplicare ogni cifra (0 e 1) per il peso che ha in ciascuna posizione e sommare il tutto. Il risultato sarà, nel nostro caso 11.

Ricapitolando ogni cifra in posizione (contate da destra verso sinistra iniziando da 0) si considera moltiplicata per 2n, anziché per 100, come si è visto per il sistema di numerazione decimale. Ad esempio, il numero binario (1011)2 corrisponde al numero decimale 11, perché 1 x 23 + 0 x 22 + 1 x 21 + 1 x 2º = 8 + 0 + 2 + 1 = 11.

Conversione Binaria Decimale

La conversione binaria decimale è sostanzialmente quello che si è visto nel paragrafo precedente, un metodo più pratico e rapido, e che si basa si quanto già spiegato è il seguente:

Numero 1 10001 Pesi 32 16 8 4 2 1 Partendo a destra da 1 riempio ogni casella dei pesi raddoppiando ogni colta il numero 1 1 0 0 0 1 32 16 8 4 2 1 32 + 16 + + 1 = 49 Seleziono solo i Pesi che nel numero binario sono ad 1, e faccio la somma.

Si prende il numero da convertire e lo si organizza in caselle come in figura, si costruiscono sotto il numero le caselle dei pesi in questo modo: si parte da destra scrivendo 1 e ogni casella a sinistra viene ottenuta dalla precedente moltiplicando per due. A questo punto si cerchiano, come in figura solo le caselle che hanno cifra 1 nel numero. Di tutte le caselle dei Pesi sottolineate si esegue la somma e si ottiene il numero in decimale.5 ISTITUTO DI ISTRUZIONE SUPERIORE polo "tecnico "G.M. DEVILLA" SASSARI

Conversione Decimale Binaria

Per la conversione da decimale a binari si ragiona in questo modo.

Cerchiamo di capirlo nel momento in qui applichiamo lo stesso ragionamento per riuscire a contare un certo numero di biglie. Supponiamo di avere 345 biglie e immaginiamo di avercele in un sacchetto e di non sapere quante sono. Come posso contarle? Posso iniziare a contarne una ad una ma non risulta un metodo molto furbo, oppure (trucco che si usava anche per contare a nascondino) le conto a gruppi di dieci. Otterrò 34 gruppi da 10 e 5 biglie in avanzo e metto ogni decina in un sacchetto. Ho stabilito che sicuramente nella cifra delle unità otterrò un 5. A questo punto separo allo stesso modo i 34 sacchetto in gruppi di dieci, otterrò 3 gruppi e 4 sacchetti in avanzo: questi sono le i sacchetti avanzati che rappresentano le decine, quindi il numero delle decine è 4. Infine i 3 gruppi da dieci sacchetti sono le centinaia ovvero 3.

Ricapitolando al primo giro ho scoperte di avere 5 unita, al secondo giro 4 decine ed infine 3 centinaia: ho scoperto che nel sacchetto c'erano 345 biglie.

Con lo stesso principio possiamo ragionare in base 2: ogni volta, piuttosto che raggrupparle per dieci, le dividiamo a gruppi di due. Dal primo accoppiamento potrà avanzare o meno una biglia e quindi stabiliremo il numero di unità binarie. Lo stesso ragionamento lo si fa con le coppie costruite al passo precedente e si vede se avanza o meno una coppia e così via.

Uno schema utile per rappresentare il ragionamento è il seguente:

• Delle 345 palline le organizza a coppie (divido per due) e ottengo 172 coppie e le metto ciascuna in un sacchettino, e mi avanza 1 pallina.

345 2 1 resto 172 divido in coppie risultato della divisione o quoto

• Adesso divido le 172 coppie in altrettante coppie, ottengo 86 nuovi sacchettini da due coppie senza avanzare niente.

345 2 1 172 2 0 resto 86 divido in coppie risultato della divisione o quoto6 ISTITUTO DI ISTRUZIONE SUPERIORE polo tecnico "G.M. DEVILLA" SASSARI

• Reitero il metodo fino ad arrivare a 0 come risultato della divisione. E ottengo lo schema come in figura:

345 2 1 172 2 0 86 2 0 43 2 1 21 2 1 10 2 0 5 2 1 2 2 0 1 2 1 0 Leggo la sequenza di 1 e 0 dall'alto verso il basso.

Logicamente essendo il primo resto quello che rappresenta l'unità (cifra di peso 0), il secondo la cifra di peso 1, il terzo la cifra di peso 3 e così via: per leggere il numero binario basterà ricopiare le cifre dal basso verso l'alto. Quindi nel nostro esempio 345 equivale a 101011001b in binario (si può usare il pedice b o 2 per far capire che è binario)

Somme tra Numeri Binari

L'addizione è una delle prime operazioni che un microprocessore riesce a fare, si tratta di comporre un circuito con diversi interruttori elettronici (transistor) organizzati in maniera tale da comporre quel dispositivo detto Adder. In questo paragrafo spiegheremo, solo dal punto di vista astratto, come viene effettuata una somma fra numeri binari.

L'addizione binaria funziona come la somma fra numeri decimali a cui siamo abituati, solo dobbiamo tenere conto che le cifre che abbiamo a disposizione sono solo 0 e 1.

Questo comporterà il fatto che 1 + 1 darà 0 con resto di 1.

Un esempio è dato dalla figura successiva (in rosso i riporti):

1 111 1 101011 + 43 + 101101 45 1011000 8 8