La medición en psicología y el análisis de datos: estadística y método científico

La medición en psicología y el análisis de datos

El análisis de datos y el método científico

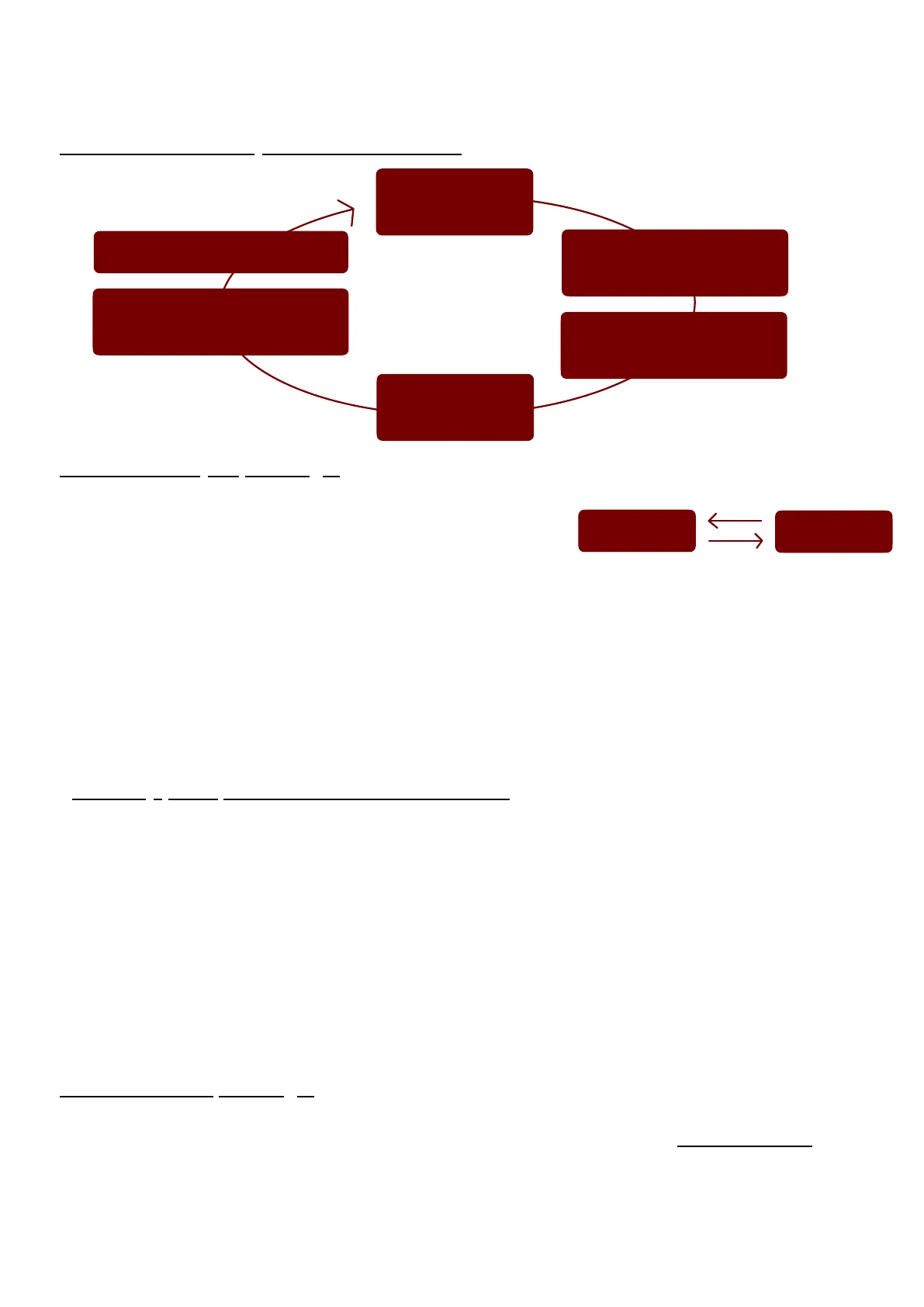
TEMA 1 LA MEDICIÓN EN PSICOLOGÍA Y EL ANÁLISIS DE DATOS 1. El análisis de datos y el método científico Planteamiento del problema Informe de investigación Deducción de hipótesis contrastables Discusión de resultados y búsqueda de conclusiones .. Procedimiento de recogida de datos Análisis de datos

La estadística y la psicología

2. La estadística y la psicología En determinados momentos de la historia, el desarrollo de la psicología se ha Estadística vinculado estrechamente al avance de la estadística, y a su vez, la estadística Psicología ha progresado influida por los avances en psicología. Se considera que el origen del empleo de métodos cuantitativos al estudiar los procesos mentales se debe a Gustav Fechner (1801-1887), planteando el problema de estudiar la relación entre la sensación y el estímulo. Desarrolló métodos para la medición de las sensaciones apoyados en aspectos estadísticos.

• Galton supuso una revolución cognitiva. Empleó técnicas estadística para estudiar diferencias individuales.
• A partir de entonces, Pearson, Spearman y Quetelet marcan la historia de la estadística.

Durante la primera mitad del siglo XX los métodos correlacionales dentro de psicología fueron dominantes. Ese mismo periodo fue el de los inicios de las técnicas descriptivas generales en la literatura psicológica. La psicología y la estadística se han beneficiado mutuamente.

¿Qué es y para qué sirve el Análisis de Datos?

3. ¿ Qué es y para qué sirve el Análisis de Datos? Se define el análisis de datos como el conjunto de procedimientos diseñados para: la selección de datos, su descripción y la extracción de conclusiones sobre ellos. Constituye una herramienta de trabajo en cualquier ciencia empírica. Pertenecen a una rama de las Matemáticas conocida con el nombre de Estadística. La Estadística está dividida en dos partes:

Estadística Descriptiva (ADI)

ESTADÍSTICA DESCRIPTIVA (ADI) Su objeto es describir las características de un conjunto de datos u observaciones (muestra). Trabaja con unos datos que se resumen en unos pocos valores descriptivos (ej: media aritmética, varianza ... ), a través de los cuales, conocemos las características de los grupos y de los individuos que los forman.

Estadística Inferencial (ADII)

ESTADÍSTICA INFERENCIAL (ADII) Consiste en inferir propiedades de una población, sobre la base de una muestra con resultados conocidos.

La medición en psicología

4. La medición en psicología Para poder utilizar el AD es necesario poder asignar números. De este proceso se encarga la "Teoría de la Medida". Pasos de la medición:

1. Identificar el objeto o sujeto a medir.
2. Identificar la propiedad o conducta que se quiere medir en el objeto o sujeto y el instrumento de medida.
3. Aplicar una regla de asignación numérica (se asigna un número a la propiedad del sujeto que se está midiendo).Para Stevens (1951), la medida es la asignación de números a objetos o sujetos según ciertas reglas. Adaptaciones:
4. Los números se asignan a las propiedades de los objetos o eventos y no a éstos en sí mismos.
5. Los números no se asignan de acuerdo con cualquier regla.

La regla tiene que garantizar que las relaciones entre los números, mantengan las relaciones que existen entre los valores de la propiedad del objeto que estemos midiendo. Ejemplo, si A pesa el doble que B, los números que describen el peso de A y B deben respetar esa diferencia. Una escala de medida se establece cuando se define el conjunto de los valores posibles que pueden asignarse a las propiedades de un objeto o sujeto y la regla de asignación que establece la correspondencia entre el sistema empírico y el sistema numérico. Cada escala permite establecer una relación distinta entre las modalidades de los distintos objetos. Tres son los problemas básicos de los que se ocupa la "Teoría Representacional de la Medida" o "Teoría de la Medida":

Representación

a) Representación Consiste en establecer las condiciones bajo las que deben construirse las escalas de medida, de modo que los números de esas escalas representen a los objetos y las relaciones empíricas entre ellos. Ejemplo, si clasificamos a las personas con respecto a su género ...

• Escala nominal: Los números (letras, símbolos) se utilizan únicamente como etiquetas de los elementos del sistema empírico. Pueden utilizarse números para representar una relación de igualdad o diferencia. Ejemplo, si clasificamos a las personas con respecto a su estrés ...
• Escala ordinal: es preciso, además de poder determinar la relación de igualdad-diferencia (como en las escalas nominales), poder determinar lo que es mayor y lo que es menor (ordenación). Ejemplo, si clasificamos días o ciudades con respecto a su temperatura ... Temperatura: Si hoy hay una Ta de 15 ° y ayer fue de 10º: -Temperaturas distintas ayer y hoy -Hoy más calor (15°) que ayer (10°) -5 º de diferencia de temperatura
• Escala de intervalo: Los números también pueden determinar la distancia o diferencia que existe entre las distintas modalidades (Igualdad/desigualdad de intervalos o distancias). Características de estas escalas: a) Origen arbitrario b) Unidad empírica de medida constante Ejemplo, si clasificamos a las personas con respecto a sus ingresos ...
• Escala de razón: Por tanto, además de las relaciones anteriores, los números también pueden representar igualdad/ desigualdad de razones, Además de lo anterior: un punto cero fijo = 0 absoluto. Por eso, a este nivel sí podemos decir que un valor es el doble o el triple que otro valor. Ejemplo, si clasificamos a las personas con respecto a su género: H = 1 y M = 2

Unicidad

b) Unicidad Hace referencia a la arbitrariedad de los números elegidos. Consiste en establecer qué transformaciones admite una escala sin perder sus características de representación (transformaciones admisibles).

• Escala nominal: transformación que preserve la igualdad-desigualdad = funciones inyectivas o isomórficas.
• Escala ordinal: transformación que preserve el orden creciente/decreciente = funciones monótonas crecientes o monotónicas.
• Escala de intervalo = funciones lineales positivas. Y = a + bx siempre que b>0
• Escala de razón = funciones multiplicativas. Y = bx siempre que b>0

Significación

c) Significación La respuesta a este problema, reside en determinar qué conclusiones o qué afirmaciones válidas se pueden hacer sobre la base de un modelo de medida. Stevens (1946), plantea la solución del problema en términos de estadísticos admisibles para cada tipo de escala.

• Escala nominal: recuento de frecuencias y la moda.
• Escala ordinal: la mediana, los percentiles.
• Escala de intervalo: la media, la varianza, el coeficiente de correlación lineal.
• Escala de razón: la media geométrica y el coeficiente de variación.

Representación Unicidad (Transformaciones Admisibles) Significación (Estadísticos Aplicables) Escala Nominal Igualdad/desigualdad Funciones inyectivas o isomórficas Frecuencia, Moda, Escala Ordinal Igualdad/desigualdad Orden Transformaciones Monótonas crecientes o monotónicas Mediana, Percentiles, Escala de Intervalo Igualdad/desigualdad Orden Igualdad de intervalos Transformaciones lineales positivas Y=a+bX, con b>0 Media, Desv. Típica, coeficiente de correlación lineal Escala de Razón Igualdad/desigualdad Orden Igualdad de intervalos Igualdad de razones Transformaciones multiplicativas Y = bX, con b>0 Media Geométrica, Coef. de Variación

Variables

5. Variables DEFINICIÓN

1. Constante; Característica que sólo puede manifestarse bajo una única modalidad. Ejemplo, si trabajamos con personas de una misma nacionalidad, esa característica se mantiene constante en ese grupo.
2. Variable; Característica que puede manifestarse según dos o más modalidades. Ejemplos, edad, género, altura, peso, etc.

CLASIFICACIÓN

1. Según su naturaleza
2. Según su nivel de medida
3. Según su papel en una investigación

Naturaleza Nivel de medida Rol en una investigación Cualitativa Cuasi-cuantitativa - Nominal Ordinal Intervalo Razón Independiente (predictora/explicativa) Dependiente (criterio/explicada) Cuantitativa Extraña(contaminadora) Especificar y describir las variables que están incluidas en una investigación es de gran importancia diseño, pruebas estadísticas ...

Definiciones

6. Definiciones POBLACIÓN Conjunto de todos los elementos que cumplen una o varias características o propiedades. Los elementos pueden ser personas, animales, objetos o números. Puede ser finita o infinita. MUESTRA Subconjunto de los elementos de una población.

Parámetro

PARÁMETRO Cualquier función de los valores de una población. Es una propiedad descriptiva de una población. Normalmente estos valores son desconocidos.

Estadístico

ESTADÍSTICO Cualquier función de los valores de una muestra. Es una propiedad descriptiva de una muestra. Son cantidades análogas a los parámetros las obtenidas en la muestra. La forma de notar los parámetros y los estadísticos es diferente. M M x estadístico Parámetro P Describir Inferencia

Notación estadística

7. Notación estadística Las variables estadísticas:

1. Se simbolizan mediante letras mayúsculas latinas: Xi, Yi, Zi.
2. Llevan asociado el subíndice "i", (las distingue de las constantes e indica la posición que ocupa un valor en el conjunto de valores de la variable. Ejemplo, Supongamos que una variable Xi, puede adoptar los siguientes valores, donde X1 represente al primer valor (2); X2 representa al (8), etc ...: - Para indicar el último valor se utiliza el subíndice "n" . - Xi es el término general y representa a cualquier valor de la serie. 2 8 4 13 20 1 J 1 X1 X2 X3 X X

Concepto de sumatorio

CONCEPTO DE SUMATORIO Suma: Una de las operaciones aritméticas más frecuentes que se realizan con los valores de las variables. Se simboliza con el signo sumatorio, que es la letra griega sigma " ". Sea una variable Xi que adopta los valores: X1, X2, X3, ... , Xn. Las notaciones colocadas abajo y arriba del símbolo indican que i tomará, sucesivamente, los valores 1,2,3,4 ... hasta n. Es Xi = X1 + X2 + X3 + ... Xn -- > Sumar todos los valores de la variable decir, debemos sumar todas las cantidades de X empezando por i = 1 (que es X1) hasta i = n (que es Xn).

Propiedades del sumatorio

PROPIEDADES DEL SUMATORIO

1. El sumatorio de una suma es igual a la suma de los sumatorios
2. El sumatorio de una resta es igual a la resta de los sumatorios
3. El sumatorio de un producto es distinto al producto de sus sumateriosY)= EX+LY i=1 i=1
4. El sumatorio de un cuadrado es distinto al cuadrado de su sumatorior)= Ex-LY i=1 i=1 i=1
5. Si K es un constante, el sumatorio de K es igual a Σ(ΧΥ)+ ΣΧ·ΣΥ i=1 i=1
6. Si K es una cte, el sumatorio de la suma de la variable y la constante es iqual(@ x)2
7. Igual para la resta EK = n.K
8. Si K es una cte, el sumatorio del producto de la variable por la cte es igual a Σ(Χ+Κ)=ΣΧ+ΣΚ=ΣΧ +nK n n n i=1 i= i=1 i=1
9. Siendo C y K dos ctes, el sumatotio delproducto de la variable por una cte más la otra vale i=1 i=1
10. Con K cte, el sumatorio de la suma de la variable y la cte, al cuadrado es igual (X .K ) = K_ X i=1
11. Para la resta ocurre igual Σ(CX+Κ)=CΣΧ +nK Σ (Χ+Κ)2 =ΣΧ2 +2ΚΣΧ+nk2 Σ(Χ-Κ)2 =ΣΧ2 - 2ΚΣΧ +nK