Niveles de Medición: Estadística Descriptiva y Pruebas Paramétricas

Niveles de Medición

Nominal
Las propiedades de la medición nominal son;

1. Exhaustiva: implica a todas las opciones
2. A los sujetos se les asignan categorias, por lo que son mutuamente excluyentes. Es decir, la
   variable está presente o no; tiene o no una caracteristica

2
Apuntes de Estadistica Inferencial

Medición Ordinal

Las propiedades de la medición ordinal son;

1. El nivel ordinal posee transitividad, por lo que se tiene la capacidad de identificar que "esto
   es mejor o mayor que aquello", en ese sentido se pueden establecer jerarquias
2. Las distancias entre un valor y otro no son iguales

Medición Intervalar

1. El nivel de medición intervalar requiere distancias iguales entre cada valor. Por lo general
   utiliza datos cuantitativos. Por ejemplo: temperatura, atributos psicológicos (CI, nivel de
   autoestima, pruebas de conocimientos, etc.)
2. Las unidades de calificación son equivalentes en todos los puntos de la escala. Una escala de
   intervalos implica: clasificación, magnitud y unidades de tamaños iguales (Brown, 2000).
3. Se pueden hacer operaciones aritméticas
4. Cuando se le pide al sujeto que califique una situación del 0 al 10 puede tomarse como un
   nivel de medición intervalar, siempre y cuando se incluya el 0

Medición de Razón

1. La escala empieza a partir del 0 absoluto, por lo tanto incluye solo los números por su valor
   en si, por lo que no pueden existir los numeros con signo negativo. Por ejemplo: Peso
   corporal en kg., edad en años, estatura en cm.
2. Convencionalmente los datos que son de nivel absoluto o de razon son manejados como los
   datos intervalares.

Nivel Nominal

• Se asignan categorías a los sujetos, pero estas no tienen un orden específico.
• Son mutuamente excluyentes, es decir, cada sujeto pertenece a una única categoría.
• Ejemplo: Género (hombre/mujer), color de ojos (azul, verde, café).

Nivel Ordinal

• Se pueden ordenar los valores según una jerarquía, lo que permite decir que algo es
  "mejor" o "peor".

. Sin embargo, las distancias entre los valores no son iguales, lo que significa que
la diferencia entre dos categorías no es constante.

• Ejemplo: Niveles de satisfacción (bajo, medio, alto), rangos militares.

Nivel Intervalar

• Los valores se pueden ordenar (como en el nivel ordinal).
• La diferencia entre valores es constante, es decir, la distancia entre un punto y
  otro es la misma en toda la escala
• Ejemplo:
  Piensa en la temperatura medida en grados Celsius (C) o Fahrenheit (ºF).
  La diferencia entre 10°℃ y 20℃ es la misma que entre 20℃ y 30℃ (10 unidades en
  ambos casos). Esto significa que podemos decir que hay una diferenciacuantificable entre los valores. Sin embargo, el nivel intervalar no tiene un cero
  absoluto.

Nivel de Razón

• Tiene todas las propiedades del nivel intervalar, pero con la diferencia de que sí tiene
  un cero absoluto (es decir, la ausencia total de la característica medida).
• Permite realizar operaciones matemáticas más avanzadas, como multiplicación y
  división.
• Ejemplo: Peso, altura, edad, ingresos económicos.

Cero Absoluto en Niveles de Medición

Sin Cero Absoluto (Intervalar)

¿Qué significa que algo tenga o no tenga cero absoluto?
Para entenderlo mejor, comparemos los niveles intervalar y razón:

• En una escala sin cero absoluto, el valor "0" no significa la ausencia total de la
  característica medida.
• Ejemplo: Temperatura en grados Celsius o Fahrenheit.
  ○
  0℃ no significa que no haya temperatura, solo es un punto arbitrario en la
  escala.
  ○
  No podemos decir que 20℃ es "el doble de caliente" que 10℃ porque el cero
  en esta escala no representa la ausencia total de temperatura.

Con Cero Absoluto (Razón)

• En una escala con cero absoluto, el "0" representa la ausencia total de lo que se
  está midiendo.
• Ejemplo: Peso, edad, ingresos.
  ○
  Si algo pesa 0 kg, significa que no tiene masa.
  ○
  Si una cuenta bancaria tiene $0, significa que no hay dinero en ella.
  Si una persona tiene 0 años de edad, significa que no ha nacido.
  ○
• En este tipo de escala, sí podemos decir que 20 es el doble de 10, porque el cero
  tiene un significado real de ausencia.

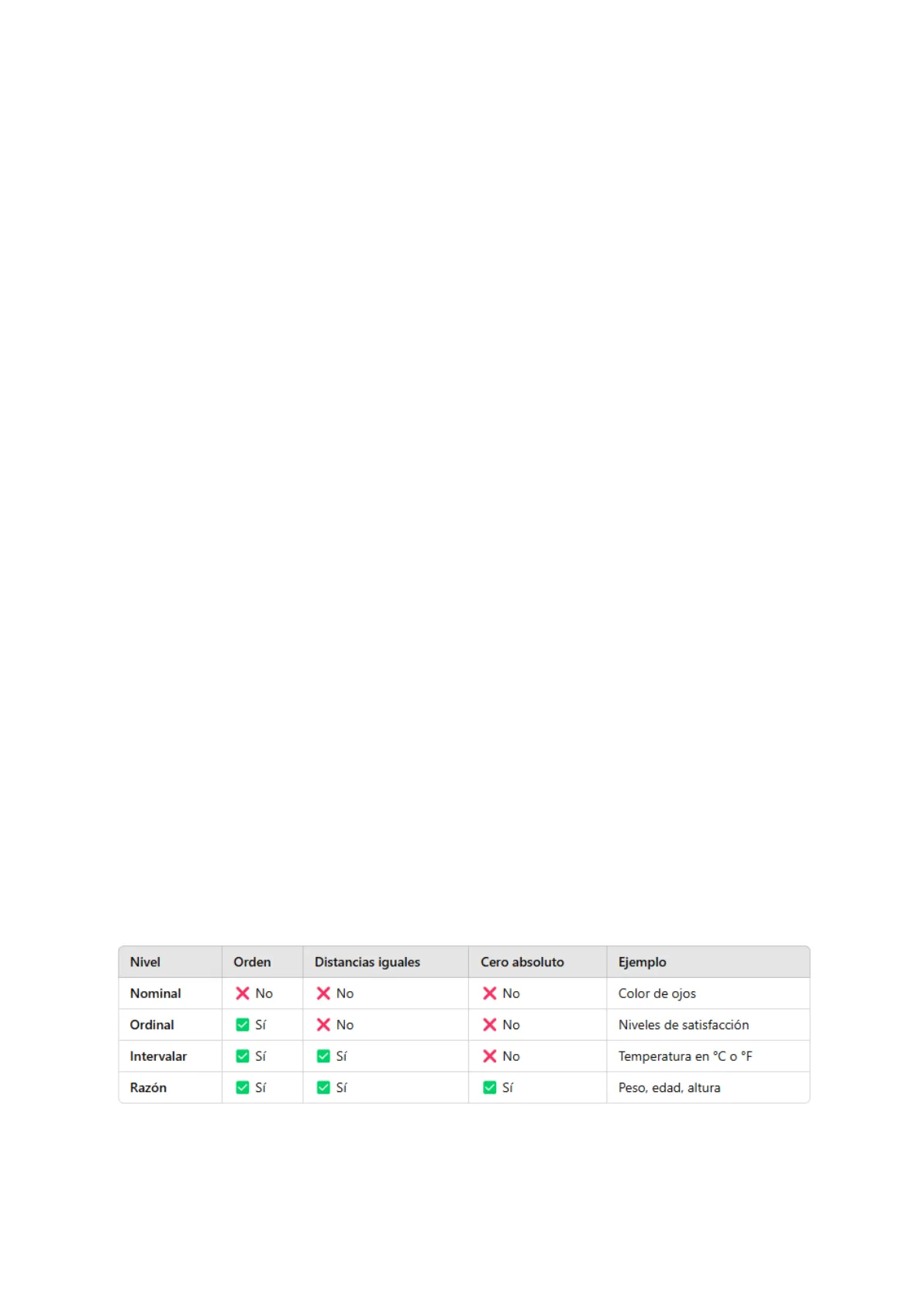
Comparativa de Niveles de Medición

Nivel
Orden
Distancias iguales
Cero absoluto
Ejemplo
Nominal
X No
X No
X
No
Color de ojos
Ordinal
Sí
X No
X
No
Niveles de satisfacción
Intervalar
Sí
Sí
X No
Temperatura en ℃ o ºF
Razón
Sí
Sí
Sí
Peso, edad, altura

Propiedades y Análisis de Niveles de Medición

Nivel
Propiedades
Medidas de
tendencia central y
dispersión
Compara
Análisis
Ejemplo
Nominal
=ó#
moda, porcentaje
Proporciones
Inferencial no paramétrica:
X2, McNemar, Coeficiente
Phi
Presencia de estrés
(si o no), Religión
Ordinal
#,=,>, <
moda, porcentajes,
mediana
Medianas
Inferencial no paramétrica:
U de Mann Whitney.
Kolmogorov Smirnoff,
Friedman, Wilcoxon, prueba
de los signos, correlación
Spearman
Calidad (Buena,
mediana, mala),
Nivel
socioeconómico
(alto, medio, bajo)
Intervalar
Distancias
iguales, = ,
>, <, 0 relativo
moda, porcentajes,
mediana, media,
desviación estándar
varianza, curtósis,
sesgo, rango, deciles,
cuartiles, percentiles
Medias
Inferencial paramétrica: t de
Student, ANOVA, regresión,
correlación Pearson
Temperatura,
atributos
psicológicos
Razón o
proporción
Igual a
intervalar, 0
absoluto
igual a intercalar
Igual a
intervalar
Igual a intervalar
Altura, Peso, Edad
en años, Grados
Kelvin

Regla del Cocodrilo para Signos de Comparación

• Imagina que el signo es la boca de un cocodrilo
• El cocodrilo siempre quiere comer el número más grande, así que abre la boca hacia
  el número mayor.
• Ejemplo:
  ○
  5 > 2 -> El 5 es más grande, así que la boca se abre hacia el.
  ○
  3 < 8 -> El 8 es más grande, así que la boca se abre hacia el.

Niveles de Medición Detallados

1. Nominal

• Propiedades: Se basa en la clasificación sin un orden específico (por
  ejemplo, "rojo", "azul", "verde"). Solo indica que algo es diferente de otra
  cosa.
• Medidas de tendencia central y dispersión: Se pueden calcular la moda (el
  valor más frecuente) y los porcentajes.
• Compara: Proporciones (porque no hay orden ni jerarquía).
• Análisis: Se usan pruebas no paramétricas, como el chi-cuadrado (x2),
  McNemar y el coeficiente Phi.
• Ejemplo: Variables como "presencia de estrés (sí o no)" o "religión".

2. Ordinal

• Propiedades: Permite ordenar los datos en una jerarquía (por ejemplo,
  "bajo", "medio", "alto"), pero sin distancias exactas entre los valores.
• Medidas de tendencia central y dispersion: Se pueden calcular la moda,
  porcentajes y la mediana.
• Compara: Medianas, ya que los valores pueden ordenarse, pero no se
  pueden hacer operaciones matemáticas como sumas o restas.

o Análisis: Se usan pruebas no paramétricas, como la U de Mann-Whitney,
Kolmogorov-Smirnov, Friedman, Wilcoxon, prueba de los signos y correlación
de Spearman.
o Ejemplo: Variables como "calidad del servicio (buena, media, mala)" o "nivel
socioeconómico (alto, medio, bajo)".

3. Intervalar

• Propiedades: Tiene orden y distancias iguales entre valores, pero no tiene
  un cero absoluto (el valor cero no indica la ausencia de la variable).
• Medidas de tendencia central y dispersión: Se pueden calcular moda,
  media, mediana, desviación estándar, varianza, curtosis, cuartiles,
  percentiles, entre otros.
• Compara: Medias, porque hay distancias iguales entre valores.
• Análisis: Se utilizan pruebas parametricas, como la t de Student, ANOVA,
  regresión y correlación de Pearson.

o Ejemplo: Variables como temperatura en grados Celsius o Fahrenheit, y
algunos atributos psicológicos.

4. Razón o Proporción

• Propiedades: Igual al nivel intervalar, pero con cero absoluto (el cero
  significa ausencia de la variable medida).
• Medidas de tendencia central y dispersión: Igual al nivel intervalar.
• Compara: Igual al nivel intervalar.
• Análisis: Igual al nivel intervalar.
• Ejemplo: Variables como altura, peso, edad en años, temperatura en
  grados Kelvin (porque el 0 absoluto indica ausencia de calor).

Nivel de Medición Nominal y Proporciones

Nota: ¿ Por que el nivel de medición nominal compara proporciones?
En el nivel nominal, los datos solo representan categorías sin orden (por ejemplo,
"femenino" o "masculino", "rojo" o "azul"). Como estas categorías no tienen una jerarquía ni
una escala numérica, no se pueden calcular medias o medianas, pero sí se pueden
calcular proporciones.
Ejemplo:
Si en una encuesta se pregunta:
"¿Tienes estrés? (Sí/No)",
podemos analizar cuántas personas respondieron "Sí" y cuántas "No", y expresar el
resultado en proporciones:

• 60% de los encuestados tienen estrés.
• 40% no tienen estrés.

La prueba estadística más común para comparar proporciones es el chi-cuadrado (x2), que
permite analizar si hay diferencias significativas entre grupos.
Ejemplo de comparación de proporciones con chi-cuadrado:
Si se quiere saber si hay una diferencia en la proporción de estrés entre hombres y mujeres,se puede aplicar esta prueba para ver si hay una asociación significativa entre el género y la
presencia de estrés.

Pruebas Paramétricas y No Paramétricas

Nota: ¿ Qué son las pruebas paramétricas y no paramétricas?
Cuando queremos analizar datos en una investigación, podemos usar diferentes tipos de
pruebas estadísticas. Estas se dividen en paramétricas y no paramétricas, dependiendo
del tipo de datos que tengamos y de ciertas condiciones que deben cumplirse.

Pruebas Paramétricas: Datos Numéricos y Distribución Normal

Las pruebas paramétricas se utilizan cuando los datos cumplen ciertas condiciones
matemáticas, como:
1. Los datos son numéricos (se pueden sumar, restar, promediar).
2. Tienen una distribución normal (cuando los datos se agrupan de forma simétrica
alrededor de la media, como la forma de una campana).
3. Hay suficientes datos (un tamaño de muestra grande permite que los resultados
sean más confiables).

• Ejemplo de distribución normal:
  Imagina que queremos medir la estatura de los estudiantes de una escuela. Si medimos a
  muchas personas, veremos que la mayoría tiene una estatura promedio y pocas personas
  son muy altas o muy bajas. Esto sigue una distribución normal.
• Ejemplos de pruebas paramétricas:
  
  • t de Student: Para comparar la media de dos grupos. (Ejemplo: comparar la altura
    promedio de hombres y mujeres).
  • ANOVA: Para comparar la media de más de dos grupos. (Ejemplo: comparar el
    promedio de calificaciones entre tres escuelas).
  • Correlación de Pearson: Para medir la relación entre dos variables numéricas.
    (Ejemplo: ver si a mayor tiempo de estudio, mayor calificación en un examen).

Cuándo Usar Pruebas Paramétricas

• Cuando los datos son numéricos.
• Cuando siguen una distribución normal.
• Cuando hay una muestra lo suficientemente grande.

Pruebas No Paramétricas: Datos sin Distribución Normal o Categóricos